The model I currently run is very simple. It is based on four independent Gaussian processes for each primary vote series: Coalition, Labor, Greens and Others. In this regard it is very similar to the two-party-preferred (TPP) model.
The model has few internal constraints and it runs reasonably fast (in about 3 and half minutes). However the parameters are sampled independently, and only sum to 100 per cent in terms of the mean/median for each parameter. For the improved speed (and the absence of pesky diagnostics) this was a worthwhile compromise.
The Stan program includes a generated quantities code block in which we convert primary vote intentions to an estimated TPP vote share, based on preference flows at previous elections.
While the TPP model operates in the range 0 to 1 (with vote share values typically between 0.45 and 0.55), the new model centers all of the primary vote observations around 100. This ensures that for each party the analysis of their vote shares are well away from the edge of valid values for all model parameters. If we did not do this, the Greens vote share (often around 0.1) would be too close to the zero parameter boundary. Stan can get grumpy if it is being asked to estimate a parameter close to a boundary.
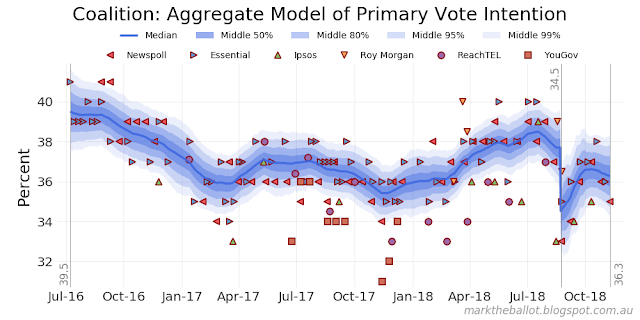
The key outputs from the new model follow. We will start with the primary vote share aggregation and an estimate of house effects for each party.
We can compare the primary vote shares for the major and minor parties.
And we can estimate the TPP vote shares for the Coalition and Labor, based on the preference flows from previous elections
The code for the latest model is as follows.
// STAN: Primary Vote Intention Model
// Essentially a set of independent Gaussian processes from day-to-day
// for each party's primary vote, centered around a mean of 100
data {
// data size
int<lower=1> n_polls;
int<lower=1> n_days;
int<lower=1> n_houses;
int<lower=1> n_parties;
real<lower=0> pseudoSampleSigma;
// Centreing factors
real<lower=0> center;
real centreing_factors[n_parties];
// poll data
real<lower=0> centered_obs_y[n_parties, n_polls]; // poll data
int<lower=1,upper=n_houses> house[n_polls]; // polling house
int<lower=1,upper=n_days> poll_day[n_polls]; // day on which polling occurred
//exclude final n parties from the sum-to-zero constraint for houseEffects
int<lower=0> n_exclude;
// period of discontinuity and subsequent increased volatility event
int<lower=1,upper=n_days> discontinuity; // start with a discontinuity
int<lower=1,upper=n_days> stability; // end - stability restored
// day-to-day change
real<lower=0> sigma;
real<lower=0> sigma_volatile;
// TPP preference flows
vector<lower=0,upper=1>[n_parties] preference_flows_2010;
vector<lower=0,upper=1>[n_parties] preference_flows_2013;
vector<lower=0,upper=1>[n_parties] preference_flows_2016;
}
transformed data {
int<lower=1> n_include = (n_houses - n_exclude);
}
parameters {
matrix[n_days, n_parties] centre_track;
matrix[n_houses, n_parties] pHouseEffects;
}
transformed parameters {
matrix[n_houses, n_parties] houseEffects;
for(p in 1:n_parties) {
houseEffects[1:n_houses, p] = pHouseEffects[1:n_houses, p] -
mean(pHouseEffects[1:n_include, p]);
}
}
model{
for (p in 1:n_parties) {
// -- house effects model
pHouseEffects[, p] ~ normal(0, 8.0); // weakly informative PRIOR
// -- temporal model - with a discontinuity followed by increased volatility
centre_track[1, p] ~ normal(center, 15); // weakly informative PRIOR
centre_track[2:(discontinuity-1), p] ~
normal(centre_track[1:(discontinuity-2), p], sigma);
centre_track[discontinuity, p] ~ normal(center, 15); // weakly informative PRIOR
centre_track[(discontinuity+1):stability, p] ~
normal(centre_track[discontinuity:(stability-1), p], sigma_volatile);
centre_track[(stability+1):n_days, p] ~
normal(centre_track[stability:(n_days-1), p], sigma);
// -- observational model
centered_obs_y[p,] ~ normal(houseEffects[house, p] +
centre_track[poll_day, p], pseudoSampleSigma);
}
}
generated quantities {
matrix[n_days, n_parties] hidden_vote_share;
vector [n_days] tpp2010;
vector [n_days] tpp2013;
vector [n_days] tpp2016;
for (p in 1:n_parties) {
hidden_vote_share[,p] = centre_track[,p] - centreing_factors[p];
}
// aggregated TPP estimates based on past preference flows
for (d in 1:n_days){
// note matrix transpose in next three lines
tpp2010[d] = sum(hidden_vote_share'[,d] .* preference_flows_2010);
tpp2013[d] = sum(hidden_vote_share'[,d] .* preference_flows_2013);
tpp2016[d] = sum(hidden_vote_share'[,d] .* preference_flows_2016);
}
}
# PYTHON: analyse primary poll data
import pandas as pd
import numpy as np
import pystan
import pickle
import sys
sys.path.append( '../bin' )
from stan_cache import stan_cache
# --- check version information
print('Python version: {}'.format(sys.version))
print('pystan version: {}'.format(pystan.__version__))
# --- curate the data for the model
# key settings
intermediate_data_dir = "./Intermediate/" # analysis saved here
# preference flows
parties = ['L/NP', 'ALP', 'GRN', 'OTH']
preference_flows_2010 = [0.9975, 0.0, 0.2116, 0.5826]
preference_flows_2013 = [0.9975, 0.0, 0.1697, 0.5330]
preference_flows_2016 = [0.9975, 0.0, 0.1806, 0.5075]
n_parties = len(parties)
# polling data
workbook = pd.ExcelFile('./Data/poll-data.xlsx')
df = workbook.parse('Data')
# drop pre-2016 election data
df['MidDate'] = [pd.Period(d, freq='D') for d in df['MidDate']]
df = df[df['MidDate'] > pd.Period('2016-07-04', freq='D')]
# push One Nation into Other
df['ONP'] = df['ONP'].fillna(0)
df['OTH'] = df['OTH'] + df['ONP']
# set start date
start = df['MidDate'].min() - 1 # the first date is day 1
df['Day'] = df['MidDate'] - start # day number for each poll
n_days = df['Day'].max() # maximum days
n_polls = len(df)
# set discontinuity date - Turnbull's last day in office
discontinuity = pd.Period('2018-08-23', freq='D') - start # UPDATE
stability = pd.Period('2018-10-01', freq='D') - start # UPDATE
# manipulate polling data ...
y = df[parties]
center = 100
centreing_factors = center - y.mean()
y = y + centreing_factors
# add polling house data to the mix
# make sure the "sum to zero" exclusions are
# last in the list
houses = df['Firm'].unique().tolist()
exclusions = ['YouGov', 'Ipsos']
# Note: we are excluding YouGov and Ipsos
# from the sum to zero constraint because
# they have unusual poll results compared
# with other pollsters
for e in exclusions:
assert(e in houses)
houses.remove(e)
houses = houses + exclusions
map = dict(zip(houses, range(1, len(houses)+1)))
df['House'] = df['Firm'].map(map)
n_houses = len(df['House'].unique())
n_exclude = len(exclusions)
# sample metrics
sampleSize = 1000 # treat all polls as being of this size
pseudoSampleSigma = np.sqrt((50 * 50) / sampleSize)
# --- compile model
# get the STAN model
with open ("./Models/primary simultaneous model.stan", "r") as f:
model = f.read()
f.close()
# encode the STAN model in C++
sm = stan_cache(model_code=model)
# --- fit the model to the data
ct_init = np.full([n_days, n_parties], center*1.0)
def initfun():
return dict(centre_track=ct_init)
chains = 5
iterations = 2000
data = {
'n_days': n_days,
'n_polls': n_polls,
'n_houses': n_houses,
'n_parties': n_parties,
'pseudoSampleSigma': pseudoSampleSigma,
'centreing_factors': centreing_factors,
'centered_obs_y': y.T,
'poll_day': df['Day'].values.tolist(),
'house': df['House'].values.tolist(),
'n_exclude': n_exclude,
'center': center,
'discontinuity': discontinuity,
'stability': stability,
# let's set the day-to-day smoothing
'sigma': 0.15,
'sigma_volatile': 0.4,
# preference flows at past elections
'preference_flows_2010': preference_flows_2010,
'preference_flows_2013': preference_flows_2013,
'preference_flows_2016': preference_flows_2016
}
fit = sm.sampling(data=data, iter=iterations, chains=chains,
init=initfun, control={'max_treedepth':13})
results = fit.extract()
# --- check diagnostics
print('Stan Finished ...')
import pystan.diagnostics as psd
print(psd.check_hmc_diagnostics(fit))
# --- save the analysis
with open(intermediate_data_dir + 'cat-' +
'output-primary-zero-sum.pkl', 'wb') as f:
pickle.dump([df,sm,fit,results,data,
centreing_factors, exclusions], f)
f.close()













No comments:
Post a Comment