More random reflections on the 2019 polls

Over the next few months, I will post some random reflections on the polls prior to the 2019 Election, and what went wrong. Today's post is a look at the two-party preferred (TPP) poll results over the past 12 months (well from 1 May 2018 to be precise). I am interested in the underlying patterns: both the periods of polling stability and when the polls changed.

With blue lines in the chart below, I have highlighted four periods when the polls look relatively stable. The first period is the last few months of the Turnbull premiership. The second period is Morrison's new premiership for the remainder of 2018. The third period is the first three months (and ten days in April) of 2019, prior to the election being called. The fourth and final period is from the dissolution of Parliament to the election. What intrigues me is the relative polling stability during each of these periods, and the marked jumps in voting intention (often over a couple of weeks) between these periods of stability.

To provide another perspective, I have plotted in red the calendar month polling averages. For the most part, these monthly averages stay close to the four period-averages I identified.

The only step change that I can clearly explain is the change from Turnbull to Morrison (immediately preceded by the Dutton challenge to Turnbull's leadership). This step change is emblematic of one of the famous aphorisms of Australian politics: disunity is death.

It is ironic to note that the highest monthly average for the year was 48.8 per cent in July 2018 under Turnbull. It is intriguing to wonder whether the polls were as out of whack in July 2018 as they were in May 2019 (when they collectively failed to foreshadow a Coalition TPP vote share at the 2019 election in excess of 51.5 per cent). Was Turnbull toppled for electability issues when he actually had 52 per cent of the TPP vote share?

The next step change that might be partially explainable is the last one: chronologically, it is associated with the April 2 Budget followed by the calling of the election on 11 April 2019. The Budget was a classic pre-election Budget (largess without nasties), and calling the election focuses the mind of the electorate on the outcome. However, I really do not find this explanation satisfying. Budgets are very technical documents, and people usually only understand the costs and benefits when they actually experience them. Nothing in the Budget was implemented prior to the election being called.

I am at a loss to explain the step change over the Christmas/New-Year period at the end of 2018 and the start of 2019. It was clearly a summer of increasing content with the government.

I am also intrigued by the question of whether the polls have been consistently wrong over this one-year period, or whether the polls have increasingly deviated from the population voting intention as they failed to fully comprehend Morrison's improved polling position over recent months.

Note: as usual I am relying on Wikipedia for the Australian opinion polling data.

Further analysis of poll variance

The stunning feature of the opinion polls leading up to the 2019 Federal Election is that they did not look like the statistics you would expect from independent, random-sample polls of the voting population. All sixteen polls were within one percentage point of each other. As I have indicated previously, this is much more tightly clustered than is mathematically plausible. This post explores that mathematics further.

My initial approach to testing for under-dispersion

One of the foundations of statistics is the notion that if I draw many independent and random samples from a population, the means of those many random samples will be normally distributed around the population mean (represented by the Greek letter mu \(\mu\)). This is known as the Central Limit Theorem or the Sampling Distribution of the Sample Mean. In practice, the Central Limit Theorem holds for samples of size 30 or higher.

The span or spread of the distribution of the many sample means around the population mean will depend on the size of those samples, which is usually denoted with a lower-case \(n\). Statisticians measure this spread through the standard deviation (which is usually denoted by the Greek letter sigma \(\sigma\)). With the two-party preferred voting data, the standard deviation for the sample proportions is given by the following formula:

$$\sigma = \sqrt{\frac{proportion_{CoalitionTPP} * proportion_{LaborTPP}}{n}}$$

While I have the sample sizes for most of the sixteen polls prior to the 2019 Election, I do not have the sample size for the final YouGov/Galaxy poll. Nor do I have the sample size for the Essential poll on 25–29 Apr 2019. For analytical purposes, I have assumed both surveys were of 1000 people. The sample sizes for the sixteen polls ranged from 707 to 3008. The mean sample size was 1403.

If we take the smallest poll, with a sample of 707 voters, we can use the standard deviation to see how likely it was to have a poll result in the range 48 to 49 for the Coalition. We will need to make an adjustment, as most pollsters round their results to the nearest whole percentage point before publication.

So the question we will ask is if we assume the population voting intention for the Coalition was 48.625 per cent (the arithmetic mean of the sixteen polls), what is the probability of a sample of 707 voters being in the range 47.5 to 49.5, which would round to 48 or 49 per cent?

For samples of 707 voters, and assuming the population mean was 48.625, we would only expect to see a poll result of 48 or 49 around 40 per cent of the time. This is the area under the curve from 47.5 to 49.5 on the x-axis when the entire area under the curve sums to 1 (or 100 per cent).

We can compare this with the expected distribution for the largest sample of 3008 voters. Our adjustment here is slightly different, as the pollster, in this case, rounded to the nearest half a percentage point. So we are interested in the area under the curve from 47.75 to 49.25 per cent.

Because the sample size (\(n\)) is larger, the spread of this distribution is narrower (compare the scale on the x-axis for both charts). We would expect almost 60 per cent of the samples to produce a result in the range 48 to 49 if the population mean (\(\mu\)) was 48.625 per cent.

We can extend this technique to all sixteen polls. We can find the proportion of all possible samples we would expect to generate a published poll result of 48 or 49. We can then multiply these probabilities together to get the probability that all sixteen polls would be in the range. Using this method, I estimate that there is a one in 49,706 chance that all sixteen polls should be in the range 48 to 49 for the Coalition (if the polls were independent random samples of the population, and the population mean was 48.625 per cent).

Chi-squared goodness of fit

Another approach is to apply a Chi-squared (\(\chi^2\)) test for goodness of fit to the sixteen polls. We can use this approach because the Central Limit Theorem tells us that the poll results should be normally distributed around the population mean. The Chi-squared test will tell us whether the poll results are normally distributed or not. In this case, the formula for the Chi-squared statistic is:

$$ \chi^2 = \sum_{i=1}^k {\biggl( \frac{x_i - \mu}{\sigma_i} \biggr)}^2 $$

Let's step through this equation. It is nowhere near as scary as it looks. To calculate the Chi-squared statistic, we do the following calculation for each poll:

• First, we calculate the mean deviation for the poll by taking the published poll result (\(x_i\)) and subtracting the population mean \(\mu\), which we estimated using the arithmetic mean for all of the polls. 
• We then divide the mean deviation by the standard deviation for the poll (\(\sigma_i\)), and then we
• square the result (multiply it by itself) - this ensures we get a positive statistic in respect of every poll. 

Finally, we sum these (\(k=16\)) squared results from each of the polls.

If the polls are normally distributed, the absolute difference between the poll result and the population mean (the mean deviation) should be around one standard deviation on average. For sixteen polls that were normally distributed around the population mean, we would expect a Chi-squared statistic around the number sixteen.

If the Chi-squared statistic is much less than 16, the poll results could be under-dispersed. If the Chi-squared statistic is much more than 16, then the poll results could be over-dispersed. For sixteen polls (which have 15 degrees of freedom, because our estimate for the population mean (\(\mu\)) is constrained by and comes from the 16 poll results), we would expect 99 per cent of the Chi-squared statistics to be between 4.6 and 32.8.

The Chi-squared statistic I calculate for the sixteen polls is 1.68, which is much less than the expected 16 on average. I can convert this 1.68 Chi-squared statistic to a probability for 15 degrees of freedom. When I do this, I find that if the polls were truly independent and random samples, (and therefore normally distributed), there would be a one in 108,282 chance of generating the narrow distribution of poll results we saw prior to the 2019 Federal Election. We can confidently say the published polls were under-dispersed.

Note: If I was to use the language of statistics, I would say our null hypothesis (\(H_0\)) has the sixteen poll results normally distributed around the population mean. Now if the null hypothesis is correct, I would expect the Chi-squared statistic to be in the range 4.6 and 32.8 (99 per cent of the time). However, as our Chi-squared statistic is outside this range, we reject the null hypothesis for the alternative hypothesis (\(H_a\)) that collectively, the poll results are not normally distributed.

Why the difference?

It is interesting to speculate on why there is a difference between these two approaches. While both approaches suggest the poll results were statistically unlikely, the Chi-squared test says they are twice as unlikely as the first approach. I suspect the answer comes from the rounding the pollsters apply to their raw results. This impacts on the normality of the distribution of poll results. In the Chi-squared test, I did not look at rounding.

So what went wrong?

There are really two questions here:

• Why were the polls under-dispersed; and
• On the day, why did the election result differ from the sixteen prior poll estimates?

To be honest, it is too early to tell with any certainty, for both questions. But we are starting to see statements from the pollsters that suggest where some of the problems may lie.

A first issue seems to be the increased use of online polls. There are a few issues here:

• Finding a random sample where all Australians have an equal chance of being polled - there have been suggestions of too many educated and politically active people are in the online samples.
• Resampling the same individuals from time to time - meaning the samples are not independent. (This may explain the lack of noise we see in polls in recent years). If your sample is not representative, and it is used often, then all of your poll results would be skewed.
• An over-reliance on clever analytics and weights to try and make a pool of online respondents look like the broader population.  These weights are challenging to keep accurate and reliable over time.

More generally, regardless of the polling methodology:

• the use of weighting, where some groups are under-represented in the raw sample frame can mean that sample errors get magnified.
• not having quotas and weights for all the factors that align somewhat with cohort political differences can mean polls accidentally do not sample important constituencies.

Like Kevin Bonham, I am not a fan of the following theories

• Shy Tory voters - too embarrassed to tell pollsters of their secret intention to vote for the Coalition.
• A late swing after the last poll.

Code snippet

To be transparent about how I approached this task, the python code snippet follows.

import pandas as pd 
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

import sys
sys.path.append( '../bin' )
plt.style.use('../bin/markgraph.mplstyle')

# --- Raw data
sample_sizes = (
    pd.Series([3008, 1000, 1842, 1201, 1265, 1644, 1079, 826, 
        2003, 1207, 1000, 826, 2136, 1012, 707, 1697]))
measurements = ( # for Labor:
    pd.Series([51.5, 51,   51,   51.5, 52,   51,   52,   51,  
        51,   52,   51,   51,  51,   52,   51,  52]))
roundings =   (
    pd.Series([0.25, 0.5,  0.5,  0.25, 0.5,  0.5,  0.5,  0.5, 
        0.5,  0.5,  0.5,  0.5, 0.5,  0.5,  0.5, 0.5]))

# some pre-processing
Mean_Labor = measurements.mean()
Mean_Coalition = 100 - Mean_Labor
variances = (measurements * (100-measurements)) / sample_sizes 
standard_deviations = pd.Series(np.sqrt(variances)) # sigma

print('Mean measurement: ', Mean_Labor)
print('Measurement counts:\n', measurements.value_counts())
print('Sample size range from/to: ', sample_sizes.min(), 
    sample_sizes.max())
print('Mean sample size: ', sample_sizes.mean())


# --- Using normal distributions
print('-----------------------------------------------------------')
individual_probs = []
for sd, r in zip(standard_deviations.tolist(), roundings):
    individual_probs.append(stats.norm(Mean_Coalition, sd).cdf(49.0 + r) - 
        stats.norm(Mean_Coalition, sd).cdf(48.0 - r))

# print individual probabilities for each poll
print('Individual probabilities: ', individual_probs)

# product of all probabilities to calculate combined probability
probability = pd.Series(individual_probs).product()
print('Overall probability: ', probability)
print('1/Probability: ', 1/probability)


# --- Chi Squared - check normally distributed - two tailed test
print('-----------------------------------------------------------')
dof = len(measurements) - 1 ### degrees of freedom
print('Degrees of freedom: ', dof)
X = pow((measurements - Mean_Labor)/standard_deviations, 2).sum()
X_min = stats.distributions.chi2.ppf(0.005, df=dof)
X_max = stats.distributions.chi2.ppf(0.995, df=dof)
print('Expected X^2 between: ', round(X_min, 2), ' and ', round(X_max, 2))
print('X^2 statistic: ', X)
X_probability = stats.chi2.cdf(X , dof)
print('Probability: ', X_probability)
print('1/Probability: ', 1 / X_probability)


# --- Chi-squared plot
print('-----------------------------------------------------------')
x = np.linspace(0, X_min + X_max, 250)
y = pd.Series(stats.chi2(dof).pdf(x), index=x)

ax = y.plot()
ax.set_title('$\chi^2$ Distribution: degrees of freedom='+str(dof))
ax.axvline(X_min, color='royalblue')
ax.axvline(X_max, color='royalblue')
ax.axvline(X, color='orange')
ax.text(x=(X_min+X_max)/2, y=0.00, s='99% between '+str(round(X_min, 2))+
    ' and '+str(round(X_max, 2)), ha='center', va='bottom')
ax.text(x=X, y=0.01, s='$\chi^2 = '+str(round(X, 2))+'$', 
    ha='right', va='bottom', rotation=90)

ax.set_xlabel('$\chi^2$')
ax.set_ylabel('Probability') 

fig = ax.figure
fig.set_size_inches(8, 4)
fig.tight_layout(pad=1)
fig.text(0.99, 0.0025, 'marktheballot.blogspot.com.au',
        ha='right', va='bottom', fontsize='x-small', 
        fontstyle='italic', color='#999999') 
fig.savefig('./Graphs/Chi-squared.png', dpi=125) 
plt.close()


# --- some normal plots
print('-----------------------------------------------------------')
mu = Mean_Coalition

n = 707
low = 47.5
high = 49.5

sigma = np.sqrt((Mean_Labor * Mean_Coalition) / n)
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 200)
y = pd.Series(stats.norm.pdf(x, mu, sigma), index=x)

ax = y.plot()
ax.set_title('Distribution of samples: n='+str(n)+', μ='+
    str(mu)+', σ='+str(round(sigma,2)))
ax.axvline(low, color='royalblue')
ax.axvline(high, color='royalblue')
ax.text(x=low-0.5, y=0.05, s=str(round(stats.norm.cdf(low, 
    loc=mu, scale=sigma)*100.0,1))+'%', ha='right', va='center')
ax.text(x=high+0.5, y=0.05, s=str(round((1-stats.norm.cdf(high, 
    loc=mu, scale=sigma))*100.0,1))+'%', ha='left', va='center')
mid = str( round(( stats.norm.cdf(high, loc=mu, scale=sigma) - 
    stats.norm.cdf(low, loc=mu, scale=sigma) )*100.0, 1) )+'%'
ax.text(x=48.5, y=0.05, s=mid, ha='center', va='center')

ax.set_xlabel('Per cent')
ax.set_ylabel('Probability') 

fig = ax.figure
fig.set_size_inches(8, 4)
fig.tight_layout(pad=1)
fig.text(0.99, 0.0025, 'marktheballot.blogspot.com.au',
        ha='right', va='bottom', fontsize='x-small', 
        fontstyle='italic', color='#999999') 
fig.savefig('./Graphs/'+str(n)+'.png', dpi=125) 
plt.close()

# ---
n = 3008
low = 47.75
high = 49.25

sigma = np.sqrt((Mean_Labor * Mean_Coalition) / n)
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 200)
y = pd.Series(stats.norm.pdf(x, mu, sigma), index=x)

ax = y.plot()
ax.set_title('Distribution of samples: n='+str(n)+', μ='+
    str(mu)+', σ='+str(round(sigma,2)))
ax.axvline(low, color='royalblue')
ax.axvline(high, color='royalblue')
ax.text(x=low-0.25, y=0.3, s=str(round(stats.norm.cdf(low, 
    loc=mu, scale=sigma)*100.0,1))+'%', ha='right', va='center')
ax.text(x=high+0.25, y=0.3, s=str(round((1-stats.norm.cdf(high, 
    loc=mu, scale=sigma))*100.0,1))+'%', ha='left', va='center')
mid = str( round(( stats.norm.cdf(high, loc=mu, scale=sigma) - 
    stats.norm.cdf(low, loc=mu, scale=sigma) )*100.0, 1) )+'%'
ax.text(x=48.5, y=0.3, s=mid, ha='center', va='center')

ax.set_xlabel('Per cent')
ax.set_ylabel('Probability') 

fig = ax.figure
fig.set_size_inches(8, 4)
fig.tight_layout(pad=1)
fig.text(0.99, 0.0025, 'marktheballot.blogspot.com.au',
        ha='right', va='bottom', fontsize='x-small', 
        fontstyle='italic', color='#999999') 
fig.savefig('./Graphs/'+str(n)+'.png', dpi=125) 
plt.close()

Why I am troubled by the polls

A couple of days ago I made the following statement:

I must admit that the under-dispersion of the recent polls troubles me a little. If the polls were normally distributed, I would expect to see poll results outside of this one-point spread for each side. Because there is under-dispersion, I have wondered about the likelihood of a polling failure (in either direction). Has the under-dispersion come about randomly (unlikely but not impossible). Or is it an artefact of some process, such as online polling? Herding? Pollster self-censorship? Or some other process I have not identified?

Since then, we have had two more polls in the same one point range: 51/52 to 49/48 in Labor's favour. As I count it on the Wikipedia polling site, with a little bit of licence for the 6-7 April poll from Roy Morgan, there are thirteen polls in a row in the same range.

One of the probability exercises you encounter when learning statistics is the question: How likely is one to flip a coin thirteen times and throw thirteen heads in a row. The maths is not too hard. If we start with the probability of one head.

$$P(H1) = \frac{1}{2} $$

The probability of two heads in a row is

$$P(H2) = \frac{1}{2} * \frac{1}{2} = \frac{1}{4}$$

The probability of thirteen heads is

$$P(H13) = \biggl(\frac{1}{2}\biggr)^{13} = 0.0001220703125$$

So the probability of me throwing 13 heads in a row is a little higher than a one in ten thousand chance. Let's call that an improbable, but not an impossible event.

We can do something similar to see how likely it is for us to have 13 opinion polls in a row within a one-percentage-point range. (Well, actually two percentage points when you account for rounding). Let's, for the sake of the argument, assume that for the entire period the population-wide voting intention was 48.5 per cent for the Coalition. This is a generous assumption. Let's also assume that the polls each had a sample of 1000 voters, which implies a standard deviation of 1.58 percentage points.

$$SD = \frac{\sqrt{48.5*51.5}}{1000} = 1.580427157448264$$

From this, we can use python and cumulative probability distribution functions - the .cdf() method in the following code snippet - to calculate the probability of one poll (and thirteen polls in a row) being 48 or 49 per cent when the intention to vote Coalition across the whole population is 48.5 per cent.

import scipy.stats as ss
import numpy as np

sd = np.sqrt((48.5 * 51.5) / 1000)
print(sd)

pop_vote_intent = 48.5
p_1 = ss.norm(pop_vote_intent, sd).cdf(49.5) - ss.norm(pop_vote_intent, sd).cdf(47.5)
print('probability for one poll: {}'.format(p_1))

p_13 = pow(p_1, 13)
print('probability for thirteen polls in a row: {}'.format(p_13))

Which yields the following results

probability for one poll: 0.47309677092421326
probability for thirteen polls in a row: 5.947710065619661e-05

Counter-intuitively, if the population-wide voting intention is 48.5 per cent; and a pollster randomly samples 1000 voters, then the chance of the pollster publishing a result of 48 or 49 per cent is slightly less than half.

The probability of 13 polls in a row at 48 or 49 per cent is 0.000059. This is actually slightly less likely than throwing 14 heads in a row.

I get the same result if I run a simulation 100,000,000 times, where each time I draw a 1000 person sample from a population where 48.5 per cent of that population has a particular voting intention. In this simulation, I have rounded the results to the nearest whole percentage point (because that is what pollsters do).

Again we can see only 47.31 per cent of the samples would yield a population estimate of 48 or 49 per cent. More than a quarter of the poll estimates would be at 50 per cent or higher. More than a quarter of the poll estimates would be at 47 per cent or lower. The code snippet for this simulation follows.

import pandas as pd 
import numpy as np 

p = 48.5
q = 100 - p
sample_size = 1000
sd = np.sqrt((p * q) / sample_size)
n = 100_000_000
dist = (pd.Series(np.random.standard_normal(n)) * sd + p).round().value_counts().sort_index()
dist = dist / dist.sum()
print('Prob at 50% or greater', dist[dist.index >= 50.0].sum())

# - and plot results ...
ax = dist.plot.bar()
ax.set_title('Probability distribution of Samples of '+str(sample_size)+
    '\n from a population where p='+str(p)+'%')
ax.set_xlabel('Rounded Percent')
ax.set_ylabel('Probability') 
fig = ax.figure
fig.set_size_inches(8, 4)
fig.tight_layout(pad=1)
fig.text(0.99, 0.01, 'marktheballot.blogspot.com.au',
        ha='right', va='bottom', fontsize='x-small', 
        fontstyle='italic', color='#999999') 
fig.savefig('./Probabilities.png', dpi=125) 

As I see it, the latest set of opinion polls are fairly improbable. They look under-dispersed compared with what I would expect from the central limit theorem. My grandmother would have bought a lottery ticket if she encountered something this unlikely.

In my mind, this under-dispersion raises a question around the reliability of the current set of opinion polls. The critical question is whether this improbable streak of polls points to something systemic. If this streak is a random improbable event, then there are no problems. However, if this streak of polls is driven by something systemic, there may be a problem.

It also raises the question of transparency. If pollsters are using a panel for their surveys, they should tell us. If pollsters are smoothing their polls, or publishing a rolling average, they should tell us. Whatever they are doing to reduce noise in their published estimates, they should tell us.

I am not sure what is behind the narrow similarity of the most recent polls. I think pure chance is unlikely. I would like to think it is some sound mathematical practice (for example, using a panel, or some data analytics applied to a statistical estimate). But I cannot help wondering whether it reflects herding or pollster self-censorship. Or whether there is some other factor at work. I just don't know. And I remain troubled.

A systemic problem with the polls, depending on what it is, may point to a heightened possibility of an unexpected election result (in either direction).

Another polling fail

We have had a few polling fails recently in the Anglo-sphere. Two United Kingdom examples quickly come to mind: the General Election in 2015, where the polls predicted a hung parliament, and Brexit in 2016, in which remaining in the EU was the predicted winner. Closer to home we had the Queensland state election in 2015, in which the polls foreshadowed a narrow Liberal National Party win.

Today's election of Donald Trump in the United States will be added to the list of historic polling fails.

• The New York Times had the average of the polls with Clinton on 45.9 per cent to Trump's 42.8 per cent (+3.1 percentage points).  The NYT gave Clinton an 84 per cent chance of winning the Electoral College vote.
• FiveThirtyEight.com had the average of the polls with Clinton on 48.5 to Trump's 44.9 per cent (+3.6). FiveThirtyEight gave Clinton a 71.4 per cent chance of winning the Electoral College vote.
• The Princeton Election Consortium had Clinton ahead of Trump with +4.0 ± 0.6 percentage points. PEC gave Clinton a 93 per cent chance of winning the Electoral College vote.

While the count is not over, the current tally has Clinton ahead in the national popular vote by +1.1 percentage points, but losing the Electoral College vote. The most likely Electoral College tally looks like Trump with 305 Electoral College votes to Clinton's 233.

So today's big question: Why such a massive polling fail?

It will take some time to answer this question with certainty. However, I have a couple of guesses.

My first guess would be the social desirability bias. This is sometimes referred to as the "shy voter problem" or the Bradley effect. At the core of this polling problem, some voters will not admit their actual polling preference to the pollster because they fear the pollster will negatively judge that preference. It is not surprising that such a controversial figure as Donald Trump would prompt issues of social desirability in polling. Elite opinion was against Trump. Clinton labeled Trump supporters as "deplorable". No-one wants to be in that basket. Pollsters might also look at Latino voters in Florida that appear to have voted for Trump in larger numbers than expected.

The second area where I suspect pollsters will look is their voter turn-out models. Who actually voted compared with who said they would vote to pollsters. This was a very different election to the previous two Presidential elections. Turnout-out models based on previous elections may have misdirected the polling results (particularly on the basis of race and particularly in the industrial mid-west).

A final thing that might be worth looking at is herding. The final polls were close, perhaps remarkably close. This may have been natural, or it may have resulted from pollsters modulating their final outputs to be similar with each other.

Last Newspoll for 2012

Today's Australian has the last Newspoll for 2012.

The weekly Bayesian poll aggregation: 48-52

I am now in a position to publish a weekly aggregation of the national opinion polls on voting intention. The headline message from the first aggregation: following an improvement in Labor's fortunes between July and mid October, national two-party preferred (TPP) voting intention has flat-lined since mid-October. If we assume that all of the house effects sum to zero over time, then the current outcome is 48.2 to 51.8 in the Coalition's favour.

At the moment, I am aggregating five separate polls: Essential, Morgan (treating the face-to-face and phone polls separately), Newspoll and Nielsen. The polls appear in the aggregation on the mid-point date of the polling period. Because Essential's weekly polls appear twice in their weekly report (as a fortnightly aggregation), I only use every second Essential report (beginning with the most recent).

This aggregation assumes that the systemic biases across the five polling streams sum to zero. Because this is an unrealistic assumption, I also produce a chart on the relative house effects of the polling houses for the period under analysis. The distance from the house median and the zero line indicates the biases applied to or subtracted from polling houses in the above chart. (Note: These will move around over time.) You can then decide whether the estimate of the national population voting intention in the first chart needs to be adjusted up or down a touch.

As a rough indication, this outcome would see the following probabilities for the minimum number of seats won.

This is not the end point in my opinion poll analytical efforts. I have started work on a Bayesian state-space model for Australia's five most populous states. This should allow for a more accurate outcome prediction on a state-by-state basis.

House effects over time

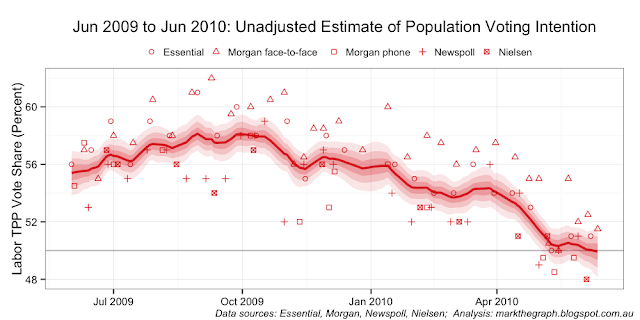
Yesterday, I looked at the house effects in the opinion polls following the elevation of Julia Gillard up until the 2010 Federal Election (actually a slightly narrower period: from 5 July to 21 August 2010). The key charts were as follows.

The house effect difference between the polling houses can be summarised in terms of relative percentage point differences as follows:

• Between Morgan face-to-face and Essential: 1.83 percentage points 
• Between Essential and Morgan phone: 0.17 percentage points 
• Between Morgan phone and Newspoll: 0.43 percentage points 
• Between Newspoll and Nielsen: 0.78 percentage points 

Unfortunately, apart from elections we cannot  benchmark the opinion polls to the actual population wide voting intention. We can, however, benchmark the polls against each other. I have adjusted my JAGS code so that the house affects must sum to zero over the period under analysis. This yields the next two charts covering the same period as the previous charts.

While this sum-to-zero constraint results in a biased estimate of population voting intentions (it's around 1 per cent pro-Labor compared with the initial election-outcome anchored analysis), the relative house effects remain largely unchanged in the analysis for the period:

• Between Morgan face-to-face and Essential: 1.83 percentage points
• Between Essential and Morgan phone: 0.16 percentage points
• Between Morgan phone and Newspoll: 0.44 percentage points
• Between Newspoll and Nielsen: 0.77 percentage points

In plain-English - the shape of the population voting curve is much the same between the two-approaches; what has changed is the vertical position of that curve.

If house effects were constant over time, it would be easy to apply this bench-marked effect to future polls. Unfortunately house effects are not constant over time. In the next three sets of charts we can see that the relativities move around - some quite markedly. The charts span three roughly one-year periods: Kevin Rudd's last 12 months as leader; calendar year 2011; and calendar year 2012.

The intriguing question I am left pondering is whether Essential has made changes to its in-house operations that have affected its relative house effects position. It also has me wondering how much I should adjust (move up or move down) the unadjusted estimate of population voting intention to get a more accurate read on the mood of the nation.

And the most recent three months ... which might just be a pretty good proxy for how the population voting trend is tracking at the moment.

Caveat: this analysis is a touch speculative.  If you see errors in my data or analytical approach, or have additional data you can give me, please drop me a line and I will re-run the analysis.

JAGS code:

    model {
        ## -- observational model
        for(i in 1:NUMPOLLS) { # for each poll result ...
            roundingEffect[i] ~ dunif(-houseRounding[i], houseRounding[i])
            yhat[i] <- houseEffect[house[i]] + walk[day[i]] + roundingEffect[i] # system
            y[i] ~ dnorm(yhat[i], samplePrecision[i]) # distribution
        }
            
        ## -- temporal model
        for(i in 2:PERIOD) { # for each day under analysis ...
            walk[i] ~ dnorm(walk[i-1], walkPrecision) # AR(1)
        }

        ## -- sum-to-zero constraint on house effects
        houseEffect[1] <- -sum( houseEffect[2:HOUSECOUNT] )
        zeroSum <- sum( houseEffect[1:HOUSECOUNT] ) # monitor

        ## -- priors
        sigmaWalk ~ dunif(0, 0.01)          ## uniform prior on std. dev.  
        walkPrecision <- pow(sigmaWalk, -2) ##   for the day-to-day random walk
        walk[1] ~ dunif(0.4, 0.6)           ## initialisation of the daily walk

        for(i in 2:HOUSECOUNT) { ## vague normal priors for house effects
            houseEffect[i] ~ dnorm(0, pow(0.1, -2))
        }
    }

House effects: a first look at the 2010 election

Following the 2004 and 2007 Federal Elections, Professor Simon Jackman published on the "house effects" of Australia's polling houses. Unfortunately, I could not find a similar analysis for the 2010 election, so for this blog I have developed a preliminary exploration of the issue.

For Jackman, house effects are the systemic biases that affect each pollster's published estimate of the population voting intention. He assumed that each published estimate from a polling house typically diverged from the from real population voting intention by a constant number of percentage points (on average and over time).

To estimate these house effects, Jackman developed a two-part model where each part of the model informed the other. Rather than outline a formal Bayesian description for Jackman's approach (with a pile of Greek letters and twiddles), I will talk through the approach.

The first part of Jackman's approach was a temporal model. It assumed that on any particular day the real population voting intention was much the same as it was on the previous day. To enable the individual house effects to be revealed, the model is anchored to the actual outcome on the election day (for the 2010 Election, the anchor would be 50.12 per cent in Labor's favour).

In the second part - the observational model - the voting intention published by a polling house for a particular date is assumed to encompass the actual population voting intention, a house effect and the margin of error for the poll.

Using a Markov chain Monte Carlo technique, Jackman identified the most likely day-to-day pathway for the temporal model for each day under analysis and the most likely house effects given the data from the observational model.

I have replicated Professor Jackman's approach in respect of the 2010 election, with a small modification to account for the different approaches to rounding taken by each polling house. I have used the TPP estimates published by the houses. Like Jackman, I used the down-rounded, mid-point date for those polls that spanned a period. As the weekly Essential reports typically aggregate two polls over a fortnight (resulting in individual weekly polls appearing twice in the Essential report data stream), I ensured that the weekly polls only appeared once in the input data to the model. Typically, this meant excluding every second Essential report.

Unfortunately, I do not have polling data for Galaxy in the lead up to the 2010 Election (if someone wants to send it to me I would be greatly appreciative). Also, I don't have the sample sizes for for all of the polls, and I have used estimates based on reasonable guesses. Consequently, this analysis must be considered incomplete. Nonetheless, my initial results follow.

In this first chart, we have the hidden temporal model estimate for each day between 5 July 2010, and the election on 21 August 2010. The red line is the median estimate from a 100,000 simulation run. The darkest zone represents the 50% credibility zone. The outer edges of the second darkest zone expands on the 50% zone to highlight the 80% credibility zone. The outer edges of the lightest zone similarly shows the 95% credibility zone.

The second chart is the estimated house effects for five of Australia's polling houses going into the 2010 Federal election. The shading in this chart has the same meaning as the previous chart. A negative value indicates that the house effect favours the Coalition. A positive value favours Labor.

The JAGS code for this analysis follows.

    model {
        ## -- observational model
        for(i in 1:length(y)) { # for each poll result ...
            roundingEffect[i] ~ dunif(-houseRounding[i], houseRounding[i])
            mu[i] <- houseEffect[house[i]] + walk[day[i]] + roundingEffect[i] # system
            y[i] ~ dnorm(mu[i], samplePrecision[i]) # distribution
        }
        
        ## -- temporal model
        for(i in 2:period) { # for each day under analysis ...
            walk[i] ~ dnorm(walk[i-1], walkPrecision) # AR(1)
        }

        ## -- priors
        sigmaWalk ~ dunif(0, 0.01)          ## uniform prior on std. dev.  
        walkPrecision <- pow(sigmaWalk, -2) ##   for the day-to-day random walk
        walk[1] ~ dunif(0.4, 0.6)           ## initialisation of the daily walk

        for(i in 1:5) {                     ## vague normal priors for house effects
            houseEffect[i] ~ dnorm(0, pow(0.1, -2))
        }
    }

Today's status quo Newspoll

Courtesy of today's Australian.

Probability of forming Majority Government

As I build a robust aggregated poll, one question I am wrestling with is how to present the findings. If we start with the trend line from my naive aggregation of the two-party preferred (TPP) polls ...

I am looking at using a Monte Carlo  technique to convert this TPP poll estimate to the probability of forming majority government. What this technique shows (below) is that the party with 51 per cent or more of the two-party preferred vote is almost guaranteed to form majority government.

There is also a realm where the two-party preferred vote is close to 50-50. In this realm, the likely outcome is a hung Parliament. When both lines fall below the 50 per cent threshold, this model is predicting a hung Parliament.

Australian 5 Poll Aggregation

I have spend the past week collecting polling data from the major polling houses. Nonetheless, I still have a ways to go in my project of building a Bayesian-intelligent aggregated poll model. Indeed, I have a ways to go on the simple task of data collection.

I can, however, plot some naive aggregations and talk a little of their limitations. These naive aggregations take all (actually most at this stage in their development) of the published polls from houses of Essential Media, Morgan, Newspoll and Nielsen. I place a localised 90-day regression over the data (the technique is called LOESS) and voila: a naive aggregation of the opinion polls. Let's have a look. We start with the aggregations of the primary vote share.

And on to the two-party-preferred aggregations.

So what are the problems with these naive aggregations? The first problem is that all of the individual poll reports are equally weighted in the final aggregation, regardless of the sample size of the poll. The aggregation also does not weight those polls that are consistently closer to the population mean at a point in time compared with those polls that exhibit higher volatility.

The second problem is that Essential Media is over-represented. Because its weekly reports are an aggregation of two weeks worth of polling, each weekly poll effectively appears twice in the aggregation. In the main, the other polling houses do not do this (although, Morgan does very occasionally). Essential Media also exhibits a number of artifacts that has me thinking about its sampling methodology and whether I need to make further adjustments in my final model. I should be clear here, these are not problems with the Essential Media reports; it is just a challenge when it comes to including Essential polls in a more robust aggregation.

The third problem is that the naive aggregation assumed that individual "house effects" balance each other out. Each polling house has its own approach. These differences go to hundreds of factors, including:

• whether the primary data is collected over the phone, in a face-to-face interview, or online, 
• how the questions are asked including the order in which the questions are asked,
• the options given or not given to respondents, 
• how the results are aggregated and weighted in the final report, 
• and so on. 

These differences in approach subtly influence the final poll results in a consistent manner over time. For some it manifests in a higher Greens/Other vote compared with the mainstream parties. For others it is the reverse. It also tends to give each house a very slight left or right bias in comparison with the other polling houses, While it is technically possible that the sum of these house effects may cancel out each other; with such a small number of regular polling houses in Australia, it is by no means guaranteed.

The fourth problem is that population biases are not accounted for. In most contexts there is a social desirability bias with which the pollsters must contend. When I attended an agricultural high school in south west New South Wales there was a social desirability bias among my classmates towards the Coalition. When I subsequently went to university and worked in the welfare sector there was a social desirability bias among my colleagues and co-workers towards Labor. At the national level, there is likely to be an overall bias in one direction or the other. Even if only one or two in a hundred people feel some shame or embarrassment in admitting their real polling intention to the pollster, this can affect the final results. The nasty thing about population biases is that they affect all polling houses in the same direction.

If these problems can be calibrated, they can be corrected in a more robust polling model, This would allow for a far more accurate population estimate of voting intention. An analogy can be made with a watch that is running five minutes slow. If you know that your watch is running slow, and how slow it is, you can mentally make the adjustment to arrive at meetings on time. But if you mistakenly believe your watch is on-time, you will regularly miss the start of meetings. With a more accurate estimate of voting intention, it is possible to better identify the probability of a Labor or Coalition win (or a hung Parliament) following the 2013 election.

Fortunately, there is a range of classical and Bayesian techniques that can be applied to each of the above problems. And that is what I will be working on for the next few weeks.

Caveats: please note, the above charts should be taken as an incomplete progress report. I am still cleaning the data I have collected (and I have more to collect). And these charts suffer from all of the problems I have outlined above, and then some more. Just because the aggregation says the Coalition two-party-preferred vote is currently sitting at 51.6 per cent, there is no guarantee that is the case.

And a thank you: I would like to thank George from Poliquant who shared his data with me. it helped me enormously in getting this far.

Update: As I refine my underlying production of these graphs and find errors or improvements, I am updating this page.

Nielsen

Today's Nielsen (probably the last Nielsen poll for 2012) was pretty much business as usual. In terms of how those polled said they would cast their preferences, the result was 48-52 against the government.

When the pollster applied preferences in accord with how they flowed at the last election the result was 47-53.

The primary vote story is as follows.

Newspoll 51-49 in the Coalition's favour

The Australian has released the latest Newspoll survey of voting intentions.The headline result is in line with the changing fortunes since the Coalition's peak at the end of April 2012. The Poll Bludger also has the details.

What would this mean at the next election? If the national vote was 51-49, the 100,000 election simulation suggests the most likely outcome would be a Coalition win.

The primary voting intentions were as follows. Of note is the decline in the Greens' fortunes.

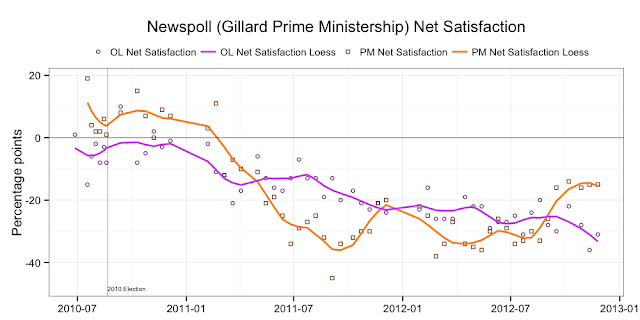
Moving to the attitudinal questions. Ms Gillard is reasserting her position as the preferred Prime Minister. Her net satisfaction rating is also improving.

And, to put a couple of those charts in some historical perspective ...