- Labor - 85 seats (they won 77 seats in 2022, in a 151 seat Parliament)
- Coalition - 36 seats (previously 58)
- Greens - 0 seats (previously 4)
- Others - 10 seats (previously 12)
- Undecided - 19 seats
Mark the Ballot
Psephology by the numbers
Sunday, May 4, 2025
Wow
Saturday, May 3, 2025
Election day - betting markets
There are two posts this morning. This is the betting market post, and separately there is a polls update.
National Winner
At 6.30am this morning, the betting market at Sportsbet was firmly of the view that the Labor Party will provide the Prime Minister in the new Parliament. The odds for a Coalition win were \$9.30 (down from \$11.00 yesterday). The odds for a Labor win were \$1.08 (up from \$1.06 yesterday). The probability of a Labor win was 89.6 per cent - down from 91.2 per cent yesterday.
Election day - polls
There are two posts this morning. This is the polls post, and separately there is a betting market update.
Two-party preferred
There is an abundance of new polls today, each with the following two-party preferred (2pp) population estimate:
- YouGov - 52.2 per cent to Labor
- Newspoll - 52.5 per cent to Labor
- Freshwater Strategy - 51.5 per cent to Labor, and
- Roy Morgan - 53 per cent to Labor.
Friday, May 2, 2025
Day 36 - 2025 Federal Election
The election is tomorrow! Today we have two more polls: Freshwater strategy 51.5/48.5 to Labor, and DemosAU 51/49 to Labor. The aggregation remains unchanged.
Thursday, May 1, 2025
Day 35 - 2025 Federal Electon
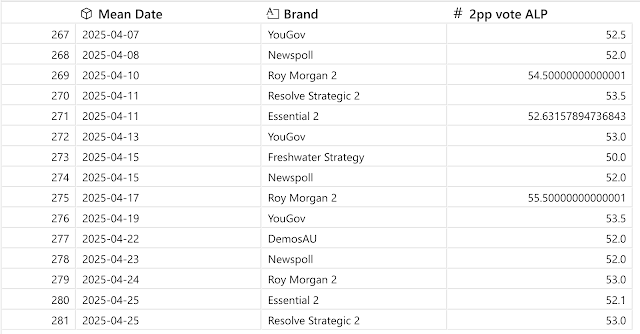
It looks like we are seeing some poll-herding in the lead-up to 2025 Election. Since yesterday's blog post, two more polls were released in the 52 to 53 per cent range for Labor. It is clear that most polls since the beginning of April are narrowly dispersed in the 52 to 53 per cent range on the two-party preferred metric for Labor.
One outlier from the narrow 52/53 trend was a Freshwater poll on 15 April which had the race at 50/50. Freshwater Strategy polls typically have the Labor vote lower than the other polls. Two outliers come from Roy Morgan: 54.5 on 10 April and 55.5 on 17 April. In recent months, Roy Morgan has typically had Labor above the trend of the other polls. A further outlier comes from Resolve Strategic with Labor on 53.5 on 11 April. And a final outlier comes from YouGov with 53.5 on 19 April.
Wednesday, April 30, 2025
Day 34 - 2025 Federal Election
Polls
Tuesday, April 29, 2025
Day 33 - 2025 Federal Election
Today we will look at a couple of new polls, and at the betting market.
New polls
Today there are two new polls to report: Roy Morgan on 53/47 to Labor, and Demos on 52/48 to Labor.