As the year draws to a close, let's have a final look at our model of the two-party preferred (TPP) vote share for 2018.
If we look over the last eight weeks, the polls have been in the usual three to four point range (in this case, with the Coalition ranging from 45 to 48 per cent). The aggregation sits within that range at 46.2 per cent. There appears to be a slight downward trend, over last eight weeks in the median aggregation estimate.
For the Coalition to give itself a better than even chance of winning a May 2019 election it will need to improve its polling position by 0.9 percentage points each month. By the end of January 2019 the Coalition would want to be on 47.1 per cent. At the and of February they would want to be at 48 per cent. At the end of March, 48.9 per cent. And at the end of April 49.8 per cent. While theoretically possible, this is an unlikely degree of sustained change in public sentiment. The more likely scenario is that the Coalition will be polling somewhere between 46 and 48 per cent of the TPP vote share come the end of April. Not enough to win.
Turning to the primate vote models ...
And our estimates of TPP based on these aggregations ...
Wednesday, December 26, 2018
Tuesday, December 4, 2018
Steady as she goes - Coalition on 46.2 per cent
Today's Essential poll (Coalition 46 v 54 Labor) has not substantially changed the Bayesian poll aggregation. I have the Coalition on 46.2 per cent of the two-party preferred vote, roughly where it has been for about two months now. If an election were held now, it is highly likely that Labor would win with a sizable majority.
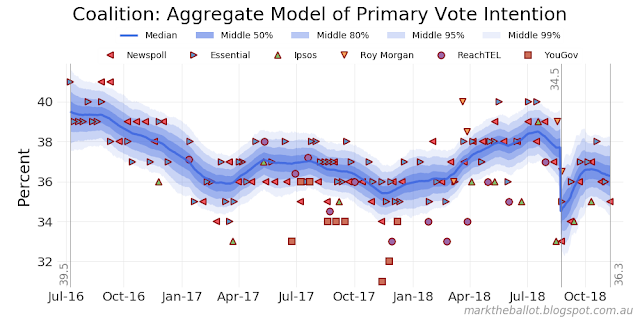
Turning to my quick and dirty aggregation of primary votes, we can see that Labor is maintaining a higher primary vote share under Morrison than it did under Turnbull, and the Coalition is maintaining a lower vote share under Morrison.
The implied two-party preferred vote share from these models is very similar to the straight aggregation above.
Turning to my quick and dirty aggregation of primary votes, we can see that Labor is maintaining a higher primary vote share under Morrison than it did under Turnbull, and the Coalition is maintaining a lower vote share under Morrison.
The implied two-party preferred vote share from these models is very similar to the straight aggregation above.
Tuesday, November 27, 2018
Betting market at new lows for the Coalition
| House | Coalition Odds ($) | Labor Odds ($) | Coalition Win Probability (%) | |
|---|---|---|---|---|
| 2018-11-27 | BetEasy | 4.50 | 1.18 | 20.77 |
| 2018-11-27 | Ladbrokes | 3.50 | 1.25 | 26.32 |
| 2018-11-27 | Sportsbet | 4.25 | 1.16 | 21.44 |
| 2018-11-27 | William Hill | 4.25 | 1.20 | 22.02 |
Saturday, November 24, 2018
Leave one out
Ipsos has intrigued me for a while. My intuition was that it was noisier than the other polling firms. And so I was wondering, is this actually the case? And if it is the case, how should I reflect that in the polling aggregation model?
Normally, when thinking about the accuracy of polling houses we would look at past performance. However, most Australian pollsters are relatively new. Even the long-standing names have been subject to mergers and acquisitions over recent years. There is just not enough history to come to a clear view about polling accuracy.
Rather than look to the historical performance of the polling houses, I wondered whether - for each pollster - we could compare them with the aggregation of all the polls excluding that pollster (a leave one out or LOO analysis). We can then look at the Root Mean Square Error (RMSE) for each pollster compared with their peers.
Rather than remove each house from the model one-by-one, I changed the model so that polls from the "left-one-out" pollster reflected the population outcome with a standard deviation of 10 percentage points (roughly equivalent to a poll with a sample size of 30) . The other polls were treated as if they had a standard deviation of 1.6 percentage points (or a sample size of 1000).
This largely removed the influence of the LOO pollster in establishing the aggregate. However, it meant that we could calculate a median house bias, which we applied before assessing the degree of error for each polling house (after all, I was interested in noisiness of a pollster, not its unadjusted house bias). My medium term intention is to pare back the influence of noisy pollsters on the model.
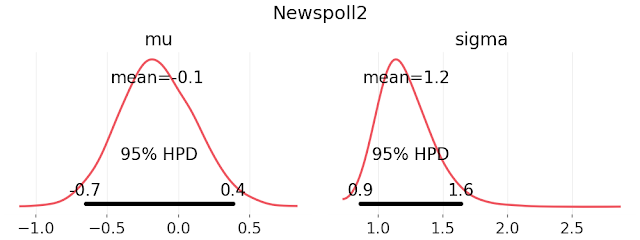
Let's look at the analysis for each pollster. being treated as uninfluential. On these charts, LOO stands for the "left one out".
Yes the differences are small. But they are also meaningful. For example, the inclusion of Ipsos drives a dip in the analysis immediately before the Turnbull/Morrison change over. No other pollster has such a dip.
Turning to the RMSE analysis: this supports the hypothesis that Ipsos is noisier than the other polling houses. For each poll I took the difference between bias adjusted poll result and the aggregate estimate on the day of the poll (in percentage points). N is the number of polls for each pollster. The mean is the mean difference. I was expecting the mean difference to be close to zero, with the differences normally distributed around zero. The standard deviation is the classical standard deviation for all of the differences. RMSE is the square root of the mean squared differences.
Because I am a Bayesian, I can use the difference data and a prior normal model to reconstruct the distribution of differences for each pollster. This yields the following parameter distributions for the difference between bias adjusted poll results and the aggregate population estimate. Again, Ipsos appears to be the noisiest of the pollsters.
For completeness, the Stan code I used in estimating the mean (mu) and standard deviation (sigma) for the difference in bias adjusted poll results when compared with the aggregate estimate from the other pollsters follows.
In terms of the model, for the more noisy pollsters, I plan to increase the noise term in the model (using the vector poll_qual_adj). In effect these pollsters will be treated as having a smaller sample size. The updated model follows.
The updated charts follow.
Normally, when thinking about the accuracy of polling houses we would look at past performance. However, most Australian pollsters are relatively new. Even the long-standing names have been subject to mergers and acquisitions over recent years. There is just not enough history to come to a clear view about polling accuracy.
Rather than look to the historical performance of the polling houses, I wondered whether - for each pollster - we could compare them with the aggregation of all the polls excluding that pollster (a leave one out or LOO analysis). We can then look at the Root Mean Square Error (RMSE) for each pollster compared with their peers.
Rather than remove each house from the model one-by-one, I changed the model so that polls from the "left-one-out" pollster reflected the population outcome with a standard deviation of 10 percentage points (roughly equivalent to a poll with a sample size of 30) . The other polls were treated as if they had a standard deviation of 1.6 percentage points (or a sample size of 1000).
This largely removed the influence of the LOO pollster in establishing the aggregate. However, it meant that we could calculate a median house bias, which we applied before assessing the degree of error for each polling house (after all, I was interested in noisiness of a pollster, not its unadjusted house bias). My medium term intention is to pare back the influence of noisy pollsters on the model.
Let's look at the analysis for each pollster. being treated as uninfluential. On these charts, LOO stands for the "left one out".
Yes the differences are small. But they are also meaningful. For example, the inclusion of Ipsos drives a dip in the analysis immediately before the Turnbull/Morrison change over. No other pollster has such a dip.
Turning to the RMSE analysis: this supports the hypothesis that Ipsos is noisier than the other polling houses. For each poll I took the difference between bias adjusted poll result and the aggregate estimate on the day of the poll (in percentage points). N is the number of polls for each pollster. The mean is the mean difference. I was expecting the mean difference to be close to zero, with the differences normally distributed around zero. The standard deviation is the classical standard deviation for all of the differences. RMSE is the square root of the mean squared differences.
| N | mean difference | std dev | RMSE | |
|---|---|---|---|---|
| Essential | 70.0 | -0.095937 | 0.885413 | 0.884211 |
| Ipsos | 12.0 | -0.423814 | 1.497985 | 1.556784 |
| Newspoll2 | 21.0 | -0.147582 | 1.129458 | 1.139059 |
| Roy Morgan | 5.0 | 0.290956 | 1.047105 | 1.086777 |
| ReachTEL | 13.0 | -0.001811 | 0.932127 | 0.932129 |
| YouGov | 9.0 | 0.284016 | 1.210048 | 1.242933 |
| Newspoll | 25.0 | 0.021968 | 0.897288 | 0.897557 |
Because I am a Bayesian, I can use the difference data and a prior normal model to reconstruct the distribution of differences for each pollster. This yields the following parameter distributions for the difference between bias adjusted poll results and the aggregate population estimate. Again, Ipsos appears to be the noisiest of the pollsters.
For completeness, the Stan code I used in estimating the mean (mu) and standard deviation (sigma) for the difference in bias adjusted poll results when compared with the aggregate estimate from the other pollsters follows.
// STAN: Bayesian Fit a Normal Distribution
data {
int<lower=1> N;
vector[N] y;
}
parameters {
real<lower=0> sigma;
real mu;
}
model {
sigma ~ cauchy(0, 5);
mu ~ cauchy(0, 5);
y ~ normal(mu, sigma);
}
In terms of the model, for the more noisy pollsters, I plan to increase the noise term in the model (using the vector poll_qual_adj). In effect these pollsters will be treated as having a smaller sample size. The updated model follows.
// STAN: Two-Party Preferred (TPP) Vote Intention Model
// - Updated to allow for a discontinuity event (Turnbull -> Morrison)
// - Updated to exclude some houses from the sum to zero constraint
// - Updated to reduce the influence of the noisier polling houses
data {
// data size
int<lower=1> n_polls;
int<lower=1> n_days;
int<lower=1> n_houses;
// assumed standard deviation for all polls
real<lower=0> pseudoSampleSigma;
// poll data
vector<lower=0,upper=1>[n_polls] y; // TPP vote share
int<lower=1> house[n_polls];
int<lower=1> day[n_polls];
vector<lower=0> [n_polls] poll_qual_adj; // poll quality adjustment
// period of discontinuity event
int<lower=1,upper=n_days> discontinuity;
int<lower=1,upper=n_days> stability;
// exclude final n houses from the house
// effects sum to zero constraint.
int<lower=0> n_exclude;
}
transformed data {
// fixed day-to-day standard deviation
real sigma = 0.0015;
real sigma_volatile = 0.0045;
int<lower=1> n_include = (n_houses - n_exclude);
}
parameters {
vector[n_days] hidden_vote_share;
vector[n_houses] pHouseEffects;
}
transformed parameters {
vector[n_houses] houseEffect;
houseEffect[1:n_houses] = pHouseEffects[1:n_houses] -
mean(pHouseEffects[1:n_include]);
}
model {
// -- temporal model [this is the hidden state-space model]
hidden_vote_share[1] ~ normal(0.5, 0.15); // PRIOR
hidden_vote_share[discontinuity] ~ normal(0.5, 0.15); // PRIOR
hidden_vote_share[2:(discontinuity-1)] ~
normal(hidden_vote_share[1:(discontinuity-2)], sigma);
hidden_vote_share[(discontinuity+1):stability] ~
normal(hidden_vote_share[discontinuity:(stability-1)], sigma_volatile);
hidden_vote_share[(stability+1):n_days] ~
normal(hidden_vote_share[stability:(n_days-1)], sigma);
// -- house effects model
pHouseEffects ~ normal(0, 0.08); // PRIOR
// -- observed data / measurement model
y ~ normal(houseEffect[house] + hidden_vote_share[day],
pseudoSampleSigma + poll_qual_adj);
}
The updated charts follow.
Tuesday, November 20, 2018
Morrison's best polls ever
Scott Morrison has just had his two best polls ever: Ipsos and Essential have both given him 48 per cent of the two party preferred vote. Although the Bayesian model has moved in the direction of the Coalition, it needs sustained polling at this level before it would be fully convinced that his vote share is actually 48 per cent.
Turning to the moving averages, which I use to cross-check the Bayesian model, we can see they are all over the place with the latest polls. It is the same message: You need more than two polls at a 48 per cent to be convinced this is the new normal (particularly in the context of the most recent Newspoll at 45 per cent).
The primary vote Bayesian models are next.
And the possible TPP from the primary models ...
Turning to the moving averages, which I use to cross-check the Bayesian model, we can see they are all over the place with the latest polls. It is the same message: You need more than two polls at a 48 per cent to be convinced this is the new normal (particularly in the context of the most recent Newspoll at 45 per cent).
The primary vote Bayesian models are next.
And the possible TPP from the primary models ...
Saturday, November 17, 2018
Updated primary vote share model
For the 2019 election, I have explored a number of models for
aggregating the primary vote shares, including models based on Dirichlet processes and centered logits. These older models were complicated and
slow. They included constraints to ensure vote shares always summed to
100 per cent for every sample from the posterior distribution.
The model I currently run is very simple. It is based on four independent Gaussian processes for each primary vote series: Coalition, Labor, Greens and Others. In this regard it is very similar to the two-party-preferred (TPP) model.
The model has few internal constraints and it runs reasonably fast (in about 3 and half minutes). However the parameters are sampled independently, and only sum to 100 per cent in terms of the mean/median for each parameter. For the improved speed (and the absence of pesky diagnostics) this was a worthwhile compromise.
The Stan program includes a generated quantities code block in which we convert primary vote intentions to an estimated TPP vote share, based on preference flows at previous elections.
While the TPP model operates in the range 0 to 1 (with vote share values typically between 0.45 and 0.55), the new model centers all of the primary vote observations around 100. This ensures that for each party the analysis of their vote shares are well away from the edge of valid values for all model parameters. If we did not do this, the Greens vote share (often around 0.1) would be too close to the zero parameter boundary. Stan can get grumpy if it is being asked to estimate a parameter close to a boundary.
The key outputs from the new model follow. We will start with the primary vote share aggregation and an estimate of house effects for each party.
We can compare the primary vote shares for the major and minor parties.
And we can estimate the TPP vote shares for the Coalition and Labor, based on the preference flows from previous elections
The code for the latest model is as follows.
The Python program to run this Stan model follows.
The model I currently run is very simple. It is based on four independent Gaussian processes for each primary vote series: Coalition, Labor, Greens and Others. In this regard it is very similar to the two-party-preferred (TPP) model.
The model has few internal constraints and it runs reasonably fast (in about 3 and half minutes). However the parameters are sampled independently, and only sum to 100 per cent in terms of the mean/median for each parameter. For the improved speed (and the absence of pesky diagnostics) this was a worthwhile compromise.
The Stan program includes a generated quantities code block in which we convert primary vote intentions to an estimated TPP vote share, based on preference flows at previous elections.
While the TPP model operates in the range 0 to 1 (with vote share values typically between 0.45 and 0.55), the new model centers all of the primary vote observations around 100. This ensures that for each party the analysis of their vote shares are well away from the edge of valid values for all model parameters. If we did not do this, the Greens vote share (often around 0.1) would be too close to the zero parameter boundary. Stan can get grumpy if it is being asked to estimate a parameter close to a boundary.
The key outputs from the new model follow. We will start with the primary vote share aggregation and an estimate of house effects for each party.
We can compare the primary vote shares for the major and minor parties.
And we can estimate the TPP vote shares for the Coalition and Labor, based on the preference flows from previous elections
The code for the latest model is as follows.
// STAN: Primary Vote Intention Model
// Essentially a set of independent Gaussian processes from day-to-day
// for each party's primary vote, centered around a mean of 100
data {
// data size
int<lower=1> n_polls;
int<lower=1> n_days;
int<lower=1> n_houses;
int<lower=1> n_parties;
real<lower=0> pseudoSampleSigma;
// Centreing factors
real<lower=0> center;
real centreing_factors[n_parties];
// poll data
real<lower=0> centered_obs_y[n_parties, n_polls]; // poll data
int<lower=1,upper=n_houses> house[n_polls]; // polling house
int<lower=1,upper=n_days> poll_day[n_polls]; // day on which polling occurred
//exclude final n parties from the sum-to-zero constraint for houseEffects
int<lower=0> n_exclude;
// period of discontinuity and subsequent increased volatility event
int<lower=1,upper=n_days> discontinuity; // start with a discontinuity
int<lower=1,upper=n_days> stability; // end - stability restored
// day-to-day change
real<lower=0> sigma;
real<lower=0> sigma_volatile;
// TPP preference flows
vector<lower=0,upper=1>[n_parties] preference_flows_2010;
vector<lower=0,upper=1>[n_parties] preference_flows_2013;
vector<lower=0,upper=1>[n_parties] preference_flows_2016;
}
transformed data {
int<lower=1> n_include = (n_houses - n_exclude);
}
parameters {
matrix[n_days, n_parties] centre_track;
matrix[n_houses, n_parties] pHouseEffects;
}
transformed parameters {
matrix[n_houses, n_parties] houseEffects;
for(p in 1:n_parties) {
houseEffects[1:n_houses, p] = pHouseEffects[1:n_houses, p] -
mean(pHouseEffects[1:n_include, p]);
}
}
model{
for (p in 1:n_parties) {
// -- house effects model
pHouseEffects[, p] ~ normal(0, 8.0); // weakly informative PRIOR
// -- temporal model - with a discontinuity followed by increased volatility
centre_track[1, p] ~ normal(center, 15); // weakly informative PRIOR
centre_track[2:(discontinuity-1), p] ~
normal(centre_track[1:(discontinuity-2), p], sigma);
centre_track[discontinuity, p] ~ normal(center, 15); // weakly informative PRIOR
centre_track[(discontinuity+1):stability, p] ~
normal(centre_track[discontinuity:(stability-1), p], sigma_volatile);
centre_track[(stability+1):n_days, p] ~
normal(centre_track[stability:(n_days-1), p], sigma);
// -- observational model
centered_obs_y[p,] ~ normal(houseEffects[house, p] +
centre_track[poll_day, p], pseudoSampleSigma);
}
}
generated quantities {
matrix[n_days, n_parties] hidden_vote_share;
vector [n_days] tpp2010;
vector [n_days] tpp2013;
vector [n_days] tpp2016;
for (p in 1:n_parties) {
hidden_vote_share[,p] = centre_track[,p] - centreing_factors[p];
}
// aggregated TPP estimates based on past preference flows
for (d in 1:n_days){
// note matrix transpose in next three lines
tpp2010[d] = sum(hidden_vote_share'[,d] .* preference_flows_2010);
tpp2013[d] = sum(hidden_vote_share'[,d] .* preference_flows_2013);
tpp2016[d] = sum(hidden_vote_share'[,d] .* preference_flows_2016);
}
}
# PYTHON: analyse primary poll data
import pandas as pd
import numpy as np
import pystan
import pickle
import sys
sys.path.append( '../bin' )
from stan_cache import stan_cache
# --- check version information
print('Python version: {}'.format(sys.version))
print('pystan version: {}'.format(pystan.__version__))
# --- curate the data for the model
# key settings
intermediate_data_dir = "./Intermediate/" # analysis saved here
# preference flows
parties = ['L/NP', 'ALP', 'GRN', 'OTH']
preference_flows_2010 = [0.9975, 0.0, 0.2116, 0.5826]
preference_flows_2013 = [0.9975, 0.0, 0.1697, 0.5330]
preference_flows_2016 = [0.9975, 0.0, 0.1806, 0.5075]
n_parties = len(parties)
# polling data
workbook = pd.ExcelFile('./Data/poll-data.xlsx')
df = workbook.parse('Data')
# drop pre-2016 election data
df['MidDate'] = [pd.Period(d, freq='D') for d in df['MidDate']]
df = df[df['MidDate'] > pd.Period('2016-07-04', freq='D')]
# push One Nation into Other
df['ONP'] = df['ONP'].fillna(0)
df['OTH'] = df['OTH'] + df['ONP']
# set start date
start = df['MidDate'].min() - 1 # the first date is day 1
df['Day'] = df['MidDate'] - start # day number for each poll
n_days = df['Day'].max() # maximum days
n_polls = len(df)
# set discontinuity date - Turnbull's last day in office
discontinuity = pd.Period('2018-08-23', freq='D') - start # UPDATE
stability = pd.Period('2018-10-01', freq='D') - start # UPDATE
# manipulate polling data ...
y = df[parties]
center = 100
centreing_factors = center - y.mean()
y = y + centreing_factors
# add polling house data to the mix
# make sure the "sum to zero" exclusions are
# last in the list
houses = df['Firm'].unique().tolist()
exclusions = ['YouGov', 'Ipsos']
# Note: we are excluding YouGov and Ipsos
# from the sum to zero constraint because
# they have unusual poll results compared
# with other pollsters
for e in exclusions:
assert(e in houses)
houses.remove(e)
houses = houses + exclusions
map = dict(zip(houses, range(1, len(houses)+1)))
df['House'] = df['Firm'].map(map)
n_houses = len(df['House'].unique())
n_exclude = len(exclusions)
# sample metrics
sampleSize = 1000 # treat all polls as being of this size
pseudoSampleSigma = np.sqrt((50 * 50) / sampleSize)
# --- compile model
# get the STAN model
with open ("./Models/primary simultaneous model.stan", "r") as f:
model = f.read()
f.close()
# encode the STAN model in C++
sm = stan_cache(model_code=model)
# --- fit the model to the data
ct_init = np.full([n_days, n_parties], center*1.0)
def initfun():
return dict(centre_track=ct_init)
chains = 5
iterations = 2000
data = {
'n_days': n_days,
'n_polls': n_polls,
'n_houses': n_houses,
'n_parties': n_parties,
'pseudoSampleSigma': pseudoSampleSigma,
'centreing_factors': centreing_factors,
'centered_obs_y': y.T,
'poll_day': df['Day'].values.tolist(),
'house': df['House'].values.tolist(),
'n_exclude': n_exclude,
'center': center,
'discontinuity': discontinuity,
'stability': stability,
# let's set the day-to-day smoothing
'sigma': 0.15,
'sigma_volatile': 0.4,
# preference flows at past elections
'preference_flows_2010': preference_flows_2010,
'preference_flows_2013': preference_flows_2013,
'preference_flows_2016': preference_flows_2016
}
fit = sm.sampling(data=data, iter=iterations, chains=chains,
init=initfun, control={'max_treedepth':13})
results = fit.extract()
# --- check diagnostics
print('Stan Finished ...')
import pystan.diagnostics as psd
print(psd.check_hmc_diagnostics(fit))
# --- save the analysis
with open(intermediate_data_dir + 'cat-' +
'output-primary-zero-sum.pkl', 'wb') as f:
pickle.dump([df,sm,fit,results,data,
centreing_factors, exclusions], f)
f.close()
Subscribe to:
Posts (Atom)