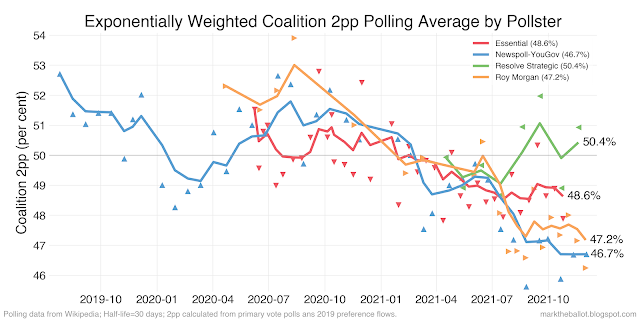
I have resurrected the Bayesian aggregation that I used at the past few elections. I have re-coded it so that the model operates in the unit scale near zero. This is not a huge change to the model, but it should work better with Stan in these terms. The model is as follows.
// STAN: Two-Party Preferred (TPP) Vote Intention Model
data {
// data size
int<lower=1> n_polls;
int<lower=1> n_days;
int<lower=1> n_houses;
// assumed standard deviation for all polls
real<lower=0> pseudoSampleSigma;
// poll data
vector<lower=-50,upper=50>[n_polls] y; // TPP vote share
int<lower=1> house[n_polls];
int<lower=1> day[n_polls];
}
transformed data {
real sigma = 0.15; // day-to-day std deviation in percentage points
}
parameters {
vector[n_days] hidden_vote_share;
vector[n_houses] pHouseEffects;
}
transformed parameters {
// -- sum to zero constraint on house effects
vector[n_houses] houseEffect;
houseEffect[1:n_houses] = pHouseEffects[1:n_houses] - mean(pHouseEffects[1:n_houses]);
}
model {
// -- temporal model [this is the hidden state-space model]
hidden_vote_share[1] ~ cauchy(0, 10); // PRIOR (reasonably uninformative)
hidden_vote_share[2:n_days] ~ normal(hidden_vote_share[1:(n_days-1)], sigma);
// -- house effects model
pHouseEffects ~ normal(0, 8); // PRIOR (reasonably uninformative)
// -- observed data / measurement model
y ~ normal(houseEffect[house] + hidden_vote_share[day], pseudoSampleSigma);
}
The key outputs from this model is a collected view of the two-party-preferred (2pp) vote share for the Coalition. All other things being equal, you would expect a Coalition 2pp vote share of 46.4 to result in a Labor landslide if the election was held now.
I have also started work on a seats model for the House of Representatives. This model will take the raw poll results and predict the number of seats each party would win. When completed, the model would also predict the probability of a hung parliament or not. To win outright, a party needs to win 76 of the 151 seats in the chamber.
The model will look at three things:
- How many seats will be won by the minor parties and independents. At the moment, I am doing this with a simple auto-regressive model. I anticipate that the number of independent and minor party seats will be the much the same as the last parliament, noting a slight tendency over time for the number of independents and minor party members to increase.
- How the two-party-preferred (2pp) outcome maps to the number of remaining seats (after minor parties and independents) won by the major parties. Quite surprisingly, the relationship is not as tight as you might think. Three times over the past 20 elections, the party with fewer 2pp votes has won a seat majority in the house.
- How the poll predictions for the 2pp at the election relate to the actual 2pp vote outcome. Last election demonstrated that sometimes the polls can have a big miss.
So far I have coded the first two parts of this model. My test outputs for a notional Coalition 2pp vote share of 47 per cent show Labor winning an outright majority around 96 per cent of the time. But, these are just test outputs from a model in development. I will back-test the model on past elections before it is finalized. The test outputs are as follows. Note: I expect the spreads to be wider on the Labor and Coalition charts once the polling uncertainty is factored into the model.




I mentioned above that the vote share only translates roughly into seats in Parliament. The next chart is the regression (and its associated confidence interval) for the relationship between 2pp vote share and seats won. The second chart is the prediction interval I use in the model. As you can see from these charts, in 1998 the then government lost by around 2 percentage points (Labor had about two percentage points more 2pp vote than the Coalition). However, the Coalition was ahead in seats by 10 percentage points. You will note that all of the past 20 elections are within the 95% prediction interval within the model.
Given the Coalition's TPP of 46.4 (which translates to a government-opposition margin of -7.2), we are in the bottom left hand corner of the previous two charts. If this does not change before the election, a change of government election is the most likely outcome.
Hopefully, I will have these models finished in the next couple of weeks.