- The Kalman Filter is designed for multivariate series - I am working with a univariate series - not a problem (and the math is much simpler), but it doesn't take advantage of the power of the Kalman Filter
- The beauty of the Kalman Filter is that it balances process control information (a mathematical model of what is expected) with measurement or sensor information - where my series is a random walk without any process control information
- In its simpler forms, it assumes that the period between sensor readings is constant - whereas poll timing is variable, with lengthy gaps over Christmas for example
- In its simpler forms, it assumes that sensor readings occur concurrently - whereas poll readings from different polling firms rarely appear on the same day, for the same period of analysis
- And in its simpler forms, the Kalman Filter is not designed for sparse sensor readings - as this results in an overly high covariance from one period to the next when there are no sensor readings - in the current case we have almost 700 days under analysis and around 100 polls from 6 pollsters.
In short, it looked like my hoped-for solution would be too difficult (at least for me) to quickly implement at a level of complexity necessary for my problem. Not all wasted, it became clear to me why the Kalman Filters others have implemented (only using polling days as the unit of analysis) were so noisy. I also realised that my Stan program has a similar issue to the last one listed above: when I use weeks rather than days as the period/unit of analysis, I get a noisier result.
I then wondered if there was another method of data fusion, which would iteratively derive an estimate of the house bias, and which could be assessed against reducing the sum of the error squared (between the smoothed aggregation and the bias-adjusted poll results). I decided to use long-term Henderson moving averages (HMA) for this purpose. [Another possibility was a LOESS or localised regression].
Before we get to that let's quickly recap the the current estimate of two-party preferred (TPP) vote share and more importantly for this exercise, the house effects. It is important to note that the house effects here are constrained to sum to zero. We have maintained that constraint in the HMA work.
The full set of April 2018 updated poll aggregates can be found here.
For the analysis, I looked at four different HMAs: 91, 181, 271 and 365 days, which is roughly 3, 6, 9 and 12 months. The resulting best fit curves for each case follows. But please note, in these charts I have not plotted the original poll results, but the bias-adjusted poll results. For example, if you look at YouGov in the above chart there are a cluster of YouGov polls at 50 per cent from July to December 2017. In the charts below, these polls have been adjusted downwards by about two and a quarter percentage points.
We can compare these results with the original Bayesian analysis as follows. Of note, the Bayesian estimate I calculate in Stan is less noisy that any of the HMAs above. Of some comfort, there is a strong sense that these lines are similar, albeit with more or less noise.
So we get to the crux of things, how does the house bias estimated in the Bayesian process by Stan compare with the quick and dirty analyses above? The following table gives the results, including the number of iterations it took to find the line of best (or at least reasonably good) fit.
| Essential | Ipsos | Newspoll | ReachTEL | Roy Morgan | YouGov | Iterations | |
|---|---|---|---|---|---|---|---|
| HMA-91 | -0.737809 | -0.730556 | -0.632002 | -0.233041 | 0.020941 | 2.312468 | 32 |
| HMA-181 | -0.756775 | -0.674001 | -0.611148 | -0.297269 | 0.106231 | 2.232961 | 4 |
| HMA-271 | -0.715895 | -0.538550 | -0.557863 | -0.295559 | -0.145591 | 2.253458 | 3 |
| HMA-365 | -0.728708 | -0.535313 | -0.562754 | -0.292410 | -0.122263 | 2.241449 | 3 |
| Bayesian Est | -0.7265 | -0.6656 | -0.5904 | -0.2619 | 0.1577 | 2.1045 | -- |
The short answer is that our results are bloody close! Not too shabby at all!
For those interested in this kind of thing, the core python code follows (minus the laborious plotting code). It is a bit messy, I have used linear algebra for some of the calculations, and others I have done in good-old-fashioned for-loops. If I wanted to be neater, I should have used linear algebra through-out. Next time I promise.
# PYHTON: iterative data fusion
# using Henderson moving averages
import pandas as pd
import numpy as np
from numpy import dot
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import sys
sys.path.append( '../bin' )
from Henderson import Henderson
from mg_plot import *
plt.style.use('../bin/markgraph.mplstyle')
# --- key constants
HMA_PERIODS = [91, 181, 271, 365] # 3, 6, 9, 12 months
graph_dir = './Graphs-HMA/'
graph_leader = 'HMA-'
intermediate_data_dir = "./Intermediate/"
# --- collect the model data
# the XL data file was extracted from the Wikipedia
# page on next Australian Federal Election
workbook = pd.ExcelFile('./Data/poll-data.xlsx')
df = workbook.parse('Data')
# drop pre-2016 election data
df['MidDate'] = [pd.Period(date, freq='D') for date in df['MidDate']]
df = df[df['MidDate'] > pd.Period('2016-07-04', freq='D')]
# convert dates to days from start
start = df['MidDate'].min() # day zero
df['Day'] = df['MidDate'] - start # day number for each poll
n_days = df['Day'].max() + 1
df = df.sort_values(by='Day')
df.index = range(len(df)) # reindex, just to be sure
# --- do for a number of different HMAs
Adjustments = pd.DataFrame()
Hidden_States = pd.DataFrame()
for HMA_PERIOD in HMA_PERIODS:
# --- iniialisation
y = (df['TPP L/NP'] / 100.0).as_matrix()
ydf = pd.DataFrame([y, df['Day'], df['Firm']],
index=['y', 'Day', 'Firm']).T
y.shape = len(y), 1 # a column vector
H = pd.get_dummies(df['Firm']) # House Effects dummy matrix
Houses = H.columns
effects = np.zeros(len(H.columns))
effects.shape = len(H.columns), 1 # a column vector
H = H.as_matrix()
# --- iteration
current_sum = np.inf
iteration_count = 0
effects = np.zeros(len(Houses))
effects.shape = len(Houses), 1 # column vector
hidden_state = pd.Series(np.array([np.nan] * n_days))
while True:
# --- save best for later
ydf_old = ydf.copy()
hidden_state_old = hidden_state.copy()
house_effects = pd.DataFrame([(-100 * effects.T)[0]],
columns=Houses, index=[['HMA-{}'.format(HMA_PERIOD)]])
house_effects['Iterations'] = [iteration_count]
# --- estimate the hidden state
ydf['adjusted_y'] = y + dot(H, effects)
hidden_state = pd.Series(np.array([np.nan] * n_days))
for day in ydf['Day'].unique():
result = ydf[ydf['Day'] == day]
hidden_state[day] = result['adjusted_y'].mean()
hidden_state = hidden_state.interpolate()
hidden_state = Henderson(hidden_state, HMA_PERIOD)
# --- update the assessment of House Effects
new_effects = []
for h in Houses:
count = 0
sum = 0
result = ydf[ydf['Firm'] == h]
for index, row in result.iterrows():
sum += hidden_state[row['Day']] - row['y']
count += 1.0
new_effects.append(sum / count)
new_effects = pd.Series(new_effects)
new_effects = new_effects - new_effects.mean() # sum to zero
effects = new_effects.values
effects.shape = len(effects), 1 # it's a column vector
# --- calculate the sum error squared for this iteration
previous_sum = current_sum
dayValue = hidden_state[ydf['Day']]
dayValue.index = ydf.index
e_row = (dayValue - ydf['adjusted_y']).values # row vector
e_col = e_row.copy()
e_col.shape = len(e_col), 1 # make a column vector
current_sum = dot(e_row, e_col)[0]
# exit if not improving solution
if (current_sum >= previous_sum):
break
iteration_count += 1
# --- get best fit - ie the previous one
ydf = ydf_old
hidden_state = hidden_state_old
# --- record house effects
Adjustments = Adjustments.append(house_effects)
Hidden_States['HMA-{}'.format(HMA_PERIOD)] = hidden_state
My Henderson Moving Average python code is here.
Update 6pm 2 April 2018
Having noted above that I could have used a localised regression rather than a Henderson moving average, I decided to have a look.And the house bias estimates ... again looking good ...
| Essential | Ipsos | Newspoll | ReachTEL | Roy Morgan | YouGov | Iterations | |
|---|---|---|---|---|---|---|---|
| LOWESS-61 | -0.736584 | -0.713434 | -0.592154 | -0.235112 | -0.029474 | 2.306759 | 3 |
| LOWESS-91 | -0.751777 | -0.676071 | -0.603489 | -0.285200 | 0.082462 | 2.234075 | 17 |
| LOWESS-181 | -0.722463 | -0.548346 | -0.552024 | -0.288691 | -0.128377 | 2.239902 | 3 |
| LOWESS-271 | -0.751364 | -0.566553 | -0.566039 | -0.288767 | -0.059591 | 2.232314 | 2 |
| Bayesian Est | -0.7265 | -0.6656 | -0.5904 | -0.2619 | 0.1577 | 2.1045 | -- |
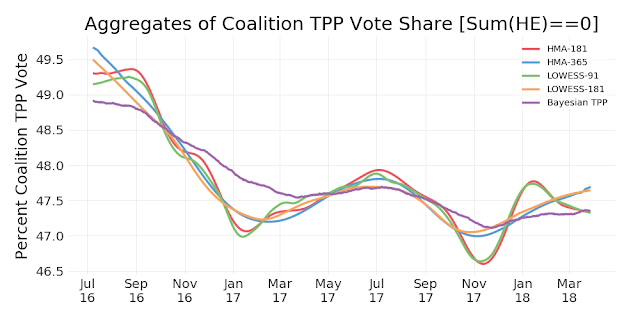
Bringing it all together in one chart ...
Which can be averaged as follows:













No comments:
Post a Comment