Yet another look at the 2010 Election

I have been thinking on how to calibrate the Bayesian aggregation to get a better understanding of the actual national two-party preferred (TPP) voting intention. At the moment, the model assumes the bias across all houses sums to zero. The model needs a constraint of some kind to work. My plan was to look at the house biases for past three or four elections and to plug a multi-election average of the biases into the model as the constraint. (Unfortunately I have been diverted from that task, and this blog post explains why).

I was also thinking about what to do with Essential, which appears under dispersed compared with what you would expect from statistical theory. Furthermore, its house effect over time is inconsistent with the effects from the other polling houses. Essential's house effect is much more variable relative to other pollsters over the long run. I would not be surprised if a lot of the behaviour we see with the Essential poll is a product of its two-stage sample frame.

Anyway, I decided to run the anchored Bayesian model for the 2010 election without Essential. The results (using 1 million iterations) were as follows. (I'd ask that you excuse the indulgence of two decimal places on the house effects chart, I know the last decimal place is mostly noise).

These results surprised me. They differed substantially to what I had seen before (replicated below with a 1,000,000 simulation run).

I asked myself, what is going on here? It was time to revisit the raw data. It was a close election and much closer than most pollsters suggested (with the final Newspoll and Essential getting the closest to predicting a hung parliament).

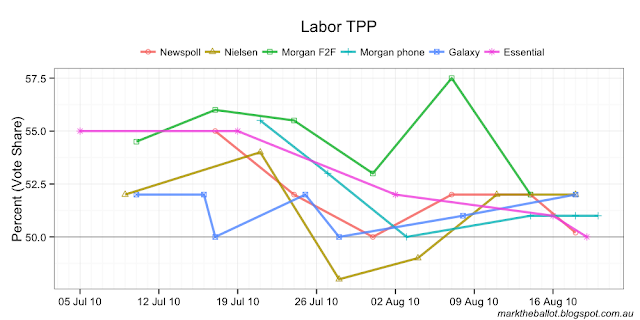
The data from the polling houses suggested very different election campaign stories. Nielsen and Galaxy paint the picture of a campaign that did not change much. The parties finished the campaign where they the started, albeit after dipping a bit in the middle.  The Essential story is one of the Coalition consistently closing the gap. Newspoll and Morgan phone also have a gap closing story, but with Labor recovering a bit before the election. Morgan phone sees the Labor recovery sustain, but Newspoll (like Essential) saw a further decline in the final week. I am not sure what to make of the Morgan F2F narrative.

These narratives can be highlighted with a short-run LOESS regression for each house.

There are a number possibilities that might explain the inconsistencies and wrinkles in and between the above charts.

There may have been a further decline in Labor's vote share in the last two days of the campaign that was not picked up by the polls. Personally, I am not convinced by this. 

I suspect the first Newspoll reading in the period was atypically high (compared with where Newspoll typically sits in house effect terms). Which means, I suspect the election was pretty close from at least month out (but before that it was more favourable for Labor with the Gillard honeymoon effect - discussed further below).

Another possibility, which I have still to explore, is that the TPP vote estimates based on preference flows in 2007 were unrealistic. 2007 was on of those turning point elections where there was a clear mood for change.  It may be that preference flows in 2010 were unusual, and my reliance on them for predicting 2013 is problematic.

A confounding factor is that Julia Gillard only replaced Kevin Rudd as Prime Minister on 24 June (less than a month before the election was announced on 17 July). The election was held in the post Gillard honeymoon period, and this may have affected some polling houses more than others. If we take a slightly longer time frame we can see the following, where it would appear that Essential and Morgan F2F were the most consistently honeymoon affected pollsters (although the Morgan phone poll had a bit of a blip there).

There is much to think about here.