We will begin with the model where house effects sum to zero, before exploring the possibility of a landslide Coalition win under the 2013 election-anchored model.
The model where house effects sum to zero
The ultimate result from the model which seeks to average house effects across parties and houses are not dissimilar to the two-party preferred (TPP) model where the house effects sum to zero.This is not that surprising. Pollsters typically use the preferences from the last election to calculate their TPP estimate. While the pollsters will have more nuanced models that allocate preferences differently by states and by the various minor parties, the net effect largely balances out.
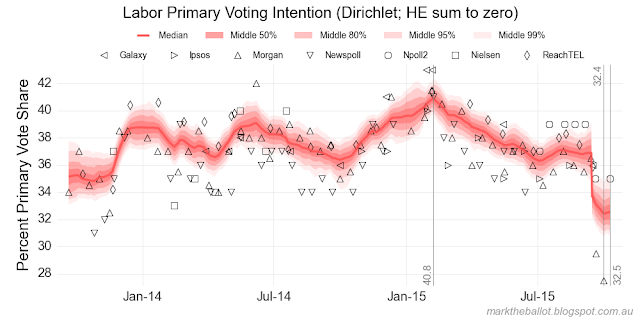
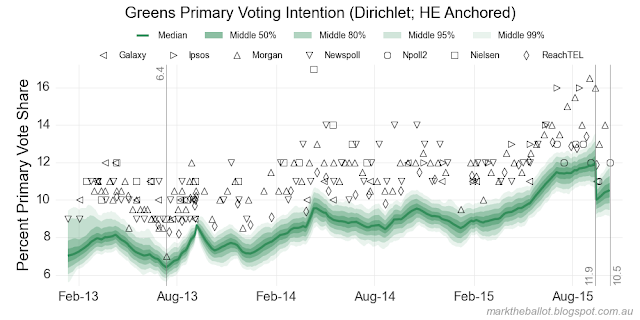
Turning to the heart of the model, we can see the median change on the discontinuity day (14-09-2015) as follows.
| Party | From (%) | To (%) | Movement (% points) |
|---|---|---|---|
| Coalition | 38.7 | 44.0 | +5.3 |
| Labor | 36.9 | 33.7 | -3.2 |
| Greens | 14.3 | 12.6 | -1.7 |
| Other | 10.1 | 9.8 | -0.3 |
In the charts we can see there has been further movement since the change of leadership. At this point I would advise caution. These poll results do not represent heart-felt voting intention. All the polls show an initial disposition to the leadership change. Without the crucible of an election, or some time for people's views to firm, these results may prove soft.
The model that produced these results follows:
model {
#### -- observational model
for(poll in 1:NUMPOLLS) { # for each poll result - rows
adjusted_poll[poll, 1:PARTIES] <- walk[pollDay[poll], 1:PARTIES] +
houseEffect[house[poll], 1:PARTIES]
primaryVotes[poll, 1:PARTIES] ~ dmulti(adjusted_poll[poll, 1:PARTIES], n[poll])
}
#### -- temporal model with one discontinuity
# - tightness of fit parameters
tightness <- 50000 # kludge - today very much like yesterday
discontinuity_tightness <- 50
# - before discontinuity
for(day in 2:(discontinuity-1)) {
# Note: use math not a distribution to generate the multinomial ...
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
# - at discontinutity
multinomial[discontinuity, 1:PARTIES] <- walk[discontinuity-1, 1:PARTIES] * discontinuity_tightness
walk[discontinuity, 1:PARTIES] ~ ddirch(multinomial[discontinuity, 1:PARTIES])
# - after discontinuity
for(day in discontinuity+1:PERIOD) {
# Note: use math not a distribution to generate the multinomial ...
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
## -- weakly informative priors for first day in the temporal model
for (party in 1:2) { # for each major party
alpha[party] ~ dunif(250, 600) # majors between 25% and 60%
}
for (party in 3:PARTIES) { # for each minor party
alpha[party] ~ dunif(10, 250) # minors between 1% and 25%
}
walk[1, 1:PARTIES] ~ ddirch(alpha[])
## -- estimate a Coalition TPP from the primary votes
for(day in 1:PERIOD) {
CoalitionTPP[day] <- sum(walk[day, 1:PARTIES] *
preference_flows[1:PARTIES])
}
#### -- sum-to-zero constraints on house effects
for (party in 2:PARTIES) { # for each party ...
# house effects across houses sum to zero
# NOTE: ALL MUST SUM TO ZERO
houseEffect[1, party] <- -sum( houseEffect[2:HOUSECOUNT, party] )
}
for(house in 1:HOUSECOUNT) { # for each house ...
# house effects across the parties sum to zero
houseEffect[house, 1] <- -sum( houseEffect[house, 2:PARTIES] )
}
# but note, we do not apply a double constraint to houseEffect[1, 1]
monitorHouseEffectOneSumParties <- sum(houseEffect[1, 1:PARTIES])
monitorHouseEffectOneSumHouses <- sum(houseEffect[1:HOUSECOUNT, 1])
## -- vague normal priors for house effects - centred on zero
for (party in 2:PARTIES) { # for each party (cols)
for(house in 2:HOUSECOUNT) { # (rows)
houseEffect[house, party] ~ dnorm(0, pow(0.1, -2))
}
}
}
The 2013 election-anchored model
Whereas the unanchored model was unsurprising, the output from the anchored model is quite surprising. In fact it is so surprising, I am not convinced that I have not made an error in my calculations. (Update: it looks like there was an error, see update below). With that caveat, let's look at the headline TPP result.A curious thing happened in the 2013 election. The primary vote polls substantially underestimated the Coalition primary vote, and over-estimated the primary vote of other parties (especially the Greens). In the TPP estimates from pollsters, this effect was muted by reduced preference flows to the Coalition in comparison with the 2010 election. The next table is the preference flows to the Coalition in 2010 and 2013.
| Year | From the Greens (%) | From other Parties(%) |
|---|---|---|
| 2010 | 21.16 | 58.26 |
| 2013 | 16.97 | 53.30 |
Returning to the primary votes, at the time of the 2013 election, the pollsters where well off the money with the Coalition and the Greens. This can be seen in the next charts, where the anchored primary vote model sits to the edge of the cloud of poll estimates, just as it did at the time of the 2013 election.
The polling house biases that underpin this model are substantial.
There are two interesting questions: First, why were the primary vote polls so far off the money in 2013? Second, are they still off the money today by the same amount?
To answer these questions, in my mind I seek to qualitatively classify elections into push factors and pull factors. I think of 2007 as a classic pull election. While Howard was a bit long in the tooth as a prime minister, the real dynamic was the new fresh face of Kevin Rudd. Rudd in 2007 attracted votes much more than Howard repelled them.
In contrast, I think of 2013 as a classic push election. Gillard and then Rudd repelled voters much more than Abbott attracted them. In this election, the people collectively voted against Gillard/Rudd rather than voting for Abbott.
As an aside, I think we have more many more push elections than pull elections. This is something that is captured in the political science aphorism: "governments tend to lose elections rather than oppositions winning them".
Returning to the first question, my suspicion is that there was a social acceptability bias against telling the pollsters that you planned to vote for the Coalition. Abbott was not a hugely popular figure, not withstanding his poll lead prior to the 2013 election. This social desirability bias saw some people who planned to vote against Labor in 2013 tell the pollster that they would vote Green, while others did not reveal their intention to vote against Labor.
In answer to the second question, I suspect that Turnbull is seen on average as more desirable (or less undesirable) than Abbott. So, over time, I expect the primary voting intention polls will be less wrong for the Coalition.
Of course, the anchored model assumes that the factors that affected polling bias in 2013 are the same factors that will affect polling bias in 2016. With the change of leadership, this is no longer the case. In addition to suspecting that Turnbull's undesirability bias is less than Abbott's, I also suspect that we will see increased preference flows to the Coalition. How these two countervailing forces will balance out is anybody's guess. But I would be surprised if Turnbull out-performs the primary-vote polls by the margin that Abbott did in 2013. I am not so sure about the TPP poll estimates based on preference flows in 2013.
Another aside: it is interesting to ponder whether the polls were as off the money for Abbott in August and early September 2015 as they were off in August and early September 2013. If they were as off the money, Abbott was in a winnable position when he was deposed. My hunch: this is unlikely. While I doubt that Shorten has the pull factor of Kevin Rudd in opposition, the memory of the Gillard/Rudd push factor would be waning with time and the Abbott push factor would have grown with time. While some voters who were put off by Rudd and Gillard would have maintained the rage; I suspect others will have moved on to wanting to remove Abbott.
Finally, let's wrap up a couple of things. We will begin with the Turnbull effect under the anchored model on the day he took the Liberal leadership. As you can see, the anchored model yields much the same net gain from different starting points.
| Party | From (%) | To (%) | Movement (% points) |
|---|---|---|---|
| Coalition | 41.3 | 46.6 | +5.3 |
| Labor | 36.4 | 33.2 | -3.2 |
| Greens | 11.9 | 10.0 | -1.9 |
| Other | 10.3 | 10.1 | -0.2 |
And, for the record, the anchored model I used.
model {
#### -- observational model
for(poll in 1:NUMPOLLS) { # for each poll result - rows
adjusted_poll[poll, 1:PARTIES] <- walk[pollDay[poll], 1:PARTIES] +
houseEffect[house[poll], 1:PARTIES]
primaryVotes[poll, 1:PARTIES] ~ dmulti(adjusted_poll[poll, 1:PARTIES], n[poll])
}
#### -- temporal model with one discontinuity
# - tightness of fit parameters
tightness <- 50000 # kludge - today very much like yesterday
discontinuity_tightness <- 50
# - before discontinuity
for(day in 2:(discontinuity-1)) {
# Note: use math not a distribution to generate the multinomial ...
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
# - at discontinutity
multinomial[discontinuity, 1:PARTIES] <- walk[discontinuity-1, 1:PARTIES] * discontinuity_tightness
walk[discontinuity, 1:PARTIES] ~ ddirch(multinomial[discontinuity, 1:PARTIES])
# - after discontinuity
for(day in discontinuity+1:PERIOD) {
# Note: use math not a distribution to generate the multinomial ...
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
## -- weakly informative priors for first day in the temporal model
for (party in 1:2) { # for each major party
alpha[party] ~ dunif(250, 600) # majors between 25% and 60%
}
for (party in 3:PARTIES) { # for each minor party
alpha[party] ~ dunif(10, 250) # minors between 1% and 25%
}
walk[1, 1:PARTIES] ~ ddirch(alpha[])
## -- estimate a Coalition TPP from the primary votes
for(day in 1:PERIOD) {
CoalitionTPP[day] <- sum(walk[day, 1:PARTIES] *
preference_flows[1:PARTIES])
}
#### -- sum-to-zero constraints on house effects
for (party in 2:PARTIES) { # for each party (cols)
for(house in 1:HOUSECOUNT) { # (rows)
houseEffect[house, party] ~ dnorm(0, pow(0.1, -2))
}
}
# need to lock in ... but only in one dimension
for(house in 1:HOUSECOUNT) { # for each house ...
# house effects across the parties sum to zero
houseEffect[house, 1] <- -sum( houseEffect[house, 2:PARTIES] )
}
}
Update (October 24, 2015)
I have refactored the way in which I calculate the discontinuity in the Hierarchical Dirichlet Process model (which I use for estimating primary vote intention). Consequently, the difference has reduced between the anchored primary vote derived two-party preferred (TPP) vote aggregation and the other TPP aggregations.The refactored model follows:
model {
#### -- observational model
for(poll in 1:NUMPOLLS) { # for each poll result - rows
adjusted_poll[poll, 1:PARTIES] <- walk[pollDay[poll], 1:PARTIES] +
houseEffect[house[poll], 1:PARTIES]
primaryVotes[poll, 1:PARTIES] ~ dmulti(adjusted_poll[poll, 1:PARTIES], n[poll])
}
#### -- temporal model with one discontinuity
# - tightness of fit parameters
tightness <- 50000 # kludge - today very much like yesterday
# - before discontinuity
for(day in 2:(discontinuity-1)) {
# Note: use of math not a distribution to generate the multinomial ...
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
# - after discontinuity
for(day in discontinuity+1:PERIOD) {
multinomial[day, 1:PARTIES] <- walk[day-1, 1:PARTIES] * tightness
walk[day, 1:PARTIES] ~ ddirch(multinomial[day, 1:PARTIES])
}
## -- weakly informative priors for first and discontinutity days
for (party in 1:2) { # for each major party
alpha[party] ~ dunif(250, 600) # majors between 25% and 60%
beta[party] ~ dunif(250, 600) # majors between 25% and 60%
}
for (party in 3:PARTIES) { # for each minor party
alpha[party] ~ dunif(10, 250) # minors between 1% and 25%
beta[party] ~ dunif(250, 600) # majors between 25% and 60%
}
walk[1, 1:PARTIES] ~ ddirch(alpha[])
walk[discontinuity, 1:PARTIES] ~ ddirch(beta[])
## -- estimate a Coalition TPP from the primary votes
for(day in 1:PERIOD) {
CoalitionTPP[day] <- sum(walk[day, 1:PARTIES] *
preference_flows[1:PARTIES])
}
#### -- sum-to-zero constraints on house effects
for (party in 2:PARTIES) { # for each party (cols)
for(house in 1:HOUSECOUNT) { # (rows)
houseEffect[house, party] ~ dnorm(0, pow(0.1, -2))
}
}
# need to lock in ... but only in one dimension
for(house in 1:HOUSECOUNT) { # for each house ...
# house effects across the parties sum to zero
houseEffect[house, 1] <- -sum( houseEffect[house, 2:PARTIES] )
}
}
















No comments:
Post a Comment